题目内容
已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0)(A在B的左边),且x1+x2=4.(1)求b的值及c的取值范围;
(2)如果AB=2,求抛物线的解析式;
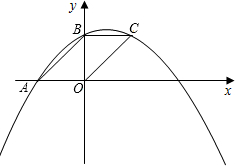
(3)设此抛物线与y轴的交点为C,顶点为D,对称轴与x轴的交点为E,问是否存在这样的抛物线,使△AOC≌BED全等,如果存在,求出抛物线的解析式;如果不存在,请说明理由.
分析:(1)由已知得:x1、x2是方程-x2+bx+c=0的两根,则△>0,及根与系数关系可求b的值及c的取值范围;
(2)由根与系数关系及AB=|x1-x2|,可求c的值;
(3)根据图形的全等分两种情况,当OC=DE时和当OC=BE时,分别讨论.
(2)由根与系数关系及AB=|x1-x2|,可求c的值;
(3)根据图形的全等分两种情况,当OC=DE时和当OC=BE时,分别讨论.
解答:解:(1)由已知得:x1、x2是方程-x2+bx+c=0的两根,
∴△=b2-4•(-1)•c>0,x1+x2=b,
又x1+x2=4,
∴b=4,c>-4;
(2)由(1)可得y=-x2+4x+c,x1+x2=4,x1•x2=-c,
而AB=|x1-x2|=2,
∴(x1-x2)2=4,
即(x1+x2)2-4x1x2=4,16+4c=4,
解得c=-3,
∴抛物线解析式为y=-x2+4x-3;
(3)存在;由(1)可得y=-x2+4x+c,
∴C(0,c),D(2,c+4);
当OC=DE时,|c|=c+4,
解得c=-2,
当OC=BE时,AB=2OC,
即|x1-x2|=2|c|,
∴(x1-x2)2=4c2;16+4c=4c2
解得c=
或
;
满足题意的抛物线解析式为:y=-x2+4x+
,y=-x2+4x+
.
∴△=b2-4•(-1)•c>0,x1+x2=b,
又x1+x2=4,
∴b=4,c>-4;
(2)由(1)可得y=-x2+4x+c,x1+x2=4,x1•x2=-c,
而AB=|x1-x2|=2,
∴(x1-x2)2=4,
即(x1+x2)2-4x1x2=4,16+4c=4,
解得c=-3,
∴抛物线解析式为y=-x2+4x-3;
(3)存在;由(1)可得y=-x2+4x+c,
∴C(0,c),D(2,c+4);
当OC=DE时,|c|=c+4,
解得c=-2,
当OC=BE时,AB=2OC,
即|x1-x2|=2|c|,
∴(x1-x2)2=4c2;16+4c=4c2
解得c=
1+
| ||
| 2 |
1-
| ||
| 2 |
满足题意的抛物线解析式为:y=-x2+4x+
1+
| ||
| 2 |
1-
| ||
| 2 |
点评:本题考查了二次函数图象和x轴的交点与一元二次方程两根的关系,掌握用两根的表达式表示线段的长度,解决全等三角形的问题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值;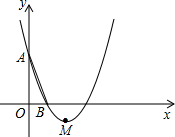 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.