题目内容
(2007•荆州)下列方程中有实数根的是( )A.x2+2x+3=0
B.x2+1=0
C.x2+3x+1=0
D.
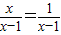
【答案】分析:本题是根的判别式的应用试题,不解方程而又准确的判断出方程解的情况,那只有根的判别式.
当△>0时,方程有两个不相等的实数根;
当△=0时,方程有两个相等的实数根;
当△<0时,方程没有实数根.
解答:解:由题意可知x2+2x+3=0
△=b2-4ac=4-12=-8<0,
所以没有是实数根;
同理x2+1=0的△=b2-4ac=0-4<0,
也没有实数根;
x2+3x+1=0的△=b2-4ac=9-4=5>0,
所以有实数根;
而最后一个去掉分母后x=1有实数根,但是使分式方程无意义,所以舍去.
故选C.
点评:本题是对方程实数根的考查,求解时一要注意是否有实数根,二要注意有实数根时是否有意义.
当△>0时,方程有两个不相等的实数根;
当△=0时,方程有两个相等的实数根;
当△<0时,方程没有实数根.
解答:解:由题意可知x2+2x+3=0
△=b2-4ac=4-12=-8<0,
所以没有是实数根;
同理x2+1=0的△=b2-4ac=0-4<0,
也没有实数根;
x2+3x+1=0的△=b2-4ac=9-4=5>0,
所以有实数根;
而最后一个去掉分母后x=1有实数根,但是使分式方程无意义,所以舍去.
故选C.
点评:本题是对方程实数根的考查,求解时一要注意是否有实数根,二要注意有实数根时是否有意义.

练习册系列答案
相关题目