题目内容
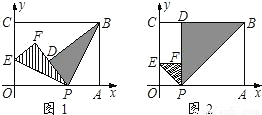
(2007•荆州)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.(1)设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;
(2)如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;
(3)在(2)的情况下,在该抛物线上是否存在点Q,使△PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.

【答案】分析:(1)由已知可得OP=x,OE=y,则PA=4-x,AB=3.利用互余关系可证Rt△POE∽Rt△BPA,由相似比可得y关于x的函数关系式;
(2)此时,△PAB、△POE均为等腰直角三角形,BD=BA=3,CD=4-3=1,故P(1,0),E(0,1),B(4,3),代入抛物线解析式的一般式即可;
(3)以PE为直角边,则点P可以作为直角顶点,此时∠EPB=90°,B点符合;点E也可以作为直角顶点,采用将直线PB向上平移过E点的方法,确定此时的直线EQ解析式,再与抛物线解析式联立,可求点Q坐标.
解答:解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠BPE=90度.
∴∠OPE+∠APB=90°.
又∵∠APB+∠ABP=90°,
∴∠OPE=∠PBA.
∴Rt△POE∽Rt△BPA.
∴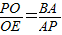 .
.
即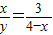 .
.
∴y= x(4-x)=-
x(4-x)=- x2+
x2+ x(0<x<4).
x(0<x<4).
且当x=2时,y有最大值 .
.
(2)由已知,△PAB、△POE均为等腰直角三角形,可得P(1,0),E(0,1),B(4,3).
设过此三点的抛物线为y=ax2+bx+c,则
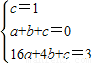
∴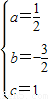
y= x2-
x2- x+1.
x+1.
(3)由(2)知∠EPB=90°,即点Q与点B重合时满足条件.
直线PB为y=x-1,与y轴交于点(0,-1).
将PB向上平移2个单位则过点E(0,1),
∴该直线为y=x+1.
由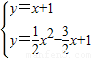
得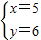
∴Q(5,6).
故该抛物线上存在两点Q(4,3)、(5,6)满足条件.
点评:本题考查了二次函数解析式的确定方法,及寻找特殊三角形条件的问题,涉及相似与平移的数学方法.
(2)此时,△PAB、△POE均为等腰直角三角形,BD=BA=3,CD=4-3=1,故P(1,0),E(0,1),B(4,3),代入抛物线解析式的一般式即可;
(3)以PE为直角边,则点P可以作为直角顶点,此时∠EPB=90°,B点符合;点E也可以作为直角顶点,采用将直线PB向上平移过E点的方法,确定此时的直线EQ解析式,再与抛物线解析式联立,可求点Q坐标.
解答:解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠BPE=90度.
∴∠OPE+∠APB=90°.
又∵∠APB+∠ABP=90°,
∴∠OPE=∠PBA.
∴Rt△POE∽Rt△BPA.
∴
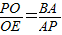 .
.即
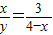 .
.∴y=
 x(4-x)=-
x(4-x)=- x2+
x2+ x(0<x<4).
x(0<x<4).且当x=2时,y有最大值
 .
.(2)由已知,△PAB、△POE均为等腰直角三角形,可得P(1,0),E(0,1),B(4,3).
设过此三点的抛物线为y=ax2+bx+c,则
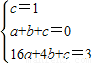
∴
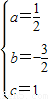
y=
 x2-
x2- x+1.
x+1.(3)由(2)知∠EPB=90°,即点Q与点B重合时满足条件.
直线PB为y=x-1,与y轴交于点(0,-1).
将PB向上平移2个单位则过点E(0,1),
∴该直线为y=x+1.
由
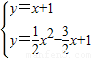
得
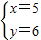
∴Q(5,6).
故该抛物线上存在两点Q(4,3)、(5,6)满足条件.
点评:本题考查了二次函数解析式的确定方法,及寻找特殊三角形条件的问题,涉及相似与平移的数学方法.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
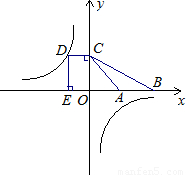
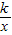 (k<0)图象上一点,过D作DC⊥y轴于C,DE⊥x轴于E,一次函数y=-x+m与y=-
(k<0)图象上一点,过D作DC⊥y轴于C,DE⊥x轴于E,一次函数y=-x+m与y=-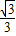 x+2的图象都过C点,与x轴分别交于A、B两点.若梯形DCAE的面积为4,求k的值.
x+2的图象都过C点,与x轴分别交于A、B两点.若梯形DCAE的面积为4,求k的值.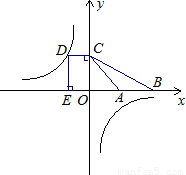
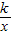 (k<0)图象上一点,过D作DC⊥y轴于C,DE⊥x轴于E,一次函数y=-x+m与y=-
(k<0)图象上一点,过D作DC⊥y轴于C,DE⊥x轴于E,一次函数y=-x+m与y=- x+2的图象都过C点,与x轴分别交于A、B两点.若梯形DCAE的面积为4,求k的值.
x+2的图象都过C点,与x轴分别交于A、B两点.若梯形DCAE的面积为4,求k的值.