题目内容
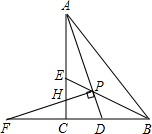 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE= S△ABP,其中正确的是
S△ABP,其中正确的是
- A.①③
- B.①②④
- C.①②③
- D.②③
C
分析:根据三角形全等的判定和性质以及三角形内角和定理逐条分析判断.
解答:在△ABC中,AD、BE分别平分∠BAC、∠ABC,
∵∠ACB=90°,
∴∠A+∠B=90°,
又∵AD、BE分别平分∠BAC、∠ABC,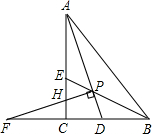
∴∠BAD+∠ABE= (∠A+∠B)=45°,
(∠A+∠B)=45°,
∴∠APB=135°,故①正确.
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
又∵∠ABP=∠FBP,
BP=BP,
∴△ABP≌△FBP,
∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.
在△APH和△FPD中,
∵∠APH=∠FPD=90°,
∠PAH=∠BAP=∠BFP,
PA=PF,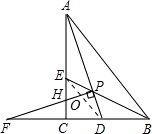
∴△APH≌△FPD,
∴AH=FD,
又∵AB=FB,
∴AB=FD+BD=AH+BD.故③正确.
∵△ABP≌△FBP,△APH≌△FPD,
∴S四边形ABDE=S△ABP+S△BDP+S△APH-S△EOH+S△DOP=S△ABP+S△ABP-S△EOH+S△DOP=2S△ABP-S△EOH+S△DOP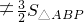 .
.
故选C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
分析:根据三角形全等的判定和性质以及三角形内角和定理逐条分析判断.
解答:在△ABC中,AD、BE分别平分∠BAC、∠ABC,
∵∠ACB=90°,
∴∠A+∠B=90°,
又∵AD、BE分别平分∠BAC、∠ABC,

∴∠BAD+∠ABE=
 (∠A+∠B)=45°,
(∠A+∠B)=45°,∴∠APB=135°,故①正确.
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
又∵∠ABP=∠FBP,
BP=BP,
∴△ABP≌△FBP,
∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.
在△APH和△FPD中,
∵∠APH=∠FPD=90°,
∠PAH=∠BAP=∠BFP,
PA=PF,

∴△APH≌△FPD,
∴AH=FD,
又∵AB=FB,
∴AB=FD+BD=AH+BD.故③正确.
∵△ABP≌△FBP,△APH≌△FPD,
∴S四边形ABDE=S△ABP+S△BDP+S△APH-S△EOH+S△DOP=S△ABP+S△ABP-S△EOH+S△DOP=2S△ABP-S△EOH+S△DOP
 .
.故选C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 10、如图,Rt△ACB中,∠ACB=90°,DE∥AB,若∠BCE=30°,则∠A=
10、如图,Rt△ACB中,∠ACB=90°,DE∥AB,若∠BCE=30°,则∠A=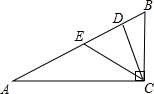 如图,Rt△ACB中,∠ACB=90°,点D、E在AB上,AC=AD,BE=BC,则∠DCE的大小是
如图,Rt△ACB中,∠ACB=90°,点D、E在AB上,AC=AD,BE=BC,则∠DCE的大小是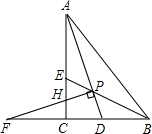 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=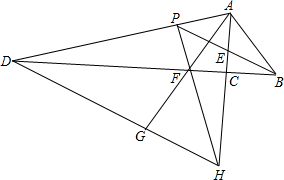 如图,Rt△ACB中,∠ACB=90°,∠ABC的角平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD-AH=AB;④DG=AP+GH.其中正确的是( )
如图,Rt△ACB中,∠ACB=90°,∠ABC的角平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD-AH=AB;④DG=AP+GH.其中正确的是( )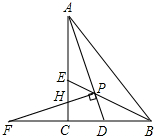 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H.
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H.