题目内容
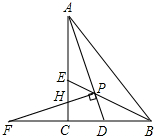 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H.
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H. 求证:①PF=PA; ②AH+BD=AB.
分析:①首先计算出∠APB=135°,进而得到∠BPD=45°,然后再计算出∠FPB=135°,然后证明△ABP≌△FBP可得PA=PF;
②首先证明∠F=∠CAD,然后证明△APH≌△FPD,进而得到AH=FD,再利用等量代换可得结论.
②首先证明∠F=∠CAD,然后证明△APH≌△FPD,进而得到AH=FD,再利用等量代换可得结论.
解答:证明:①∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=
(∠CAB+∠CBA)=45°,
∴∠APB=135°,
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA),
∴PA=PF,
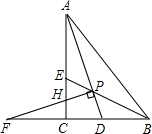
②∵△ABP≌△FBP,
∴∠BAP=∠F,
∵∠BAP=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=FD,
又∵AB=FB,
∴AB=FD+BD=AH+BD.
∴∠CAB+∠CBA=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=
| 1 |
| 2 |
∴∠APB=135°,
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
在△ABP和△FBP中,
|
∴△ABP≌△FBP(ASA),
∴PA=PF,

②∵△ABP≌△FBP,
∴∠BAP=∠F,
∵∠BAP=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
|
∴△APH≌△FPD(ASA),
∴AH=FD,
又∵AB=FB,
∴AB=FD+BD=AH+BD.
点评:此题主要考查了全等三角形的判定与性质,证明三角形全等是证明线段相等的重要手段.

练习册系列答案
相关题目
 10、如图,Rt△ACB中,∠ACB=90°,DE∥AB,若∠BCE=30°,则∠A=
10、如图,Rt△ACB中,∠ACB=90°,DE∥AB,若∠BCE=30°,则∠A=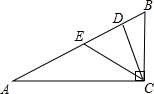 如图,Rt△ACB中,∠ACB=90°,点D、E在AB上,AC=AD,BE=BC,则∠DCE的大小是
如图,Rt△ACB中,∠ACB=90°,点D、E在AB上,AC=AD,BE=BC,则∠DCE的大小是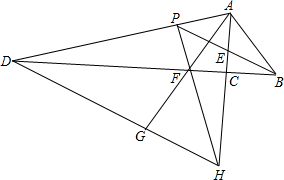 如图,Rt△ACB中,∠ACB=90°,∠ABC的角平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD-AH=AB;④DG=AP+GH.其中正确的是( )
如图,Rt△ACB中,∠ACB=90°,∠ABC的角平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD-AH=AB;④DG=AP+GH.其中正确的是( )