Question

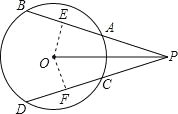
【题目】已知：如图，点P是⊙O外的一点，PB与⊙O相交于点A、B，PD与⊙O相交于C、D，AB=CD．

求证：（1）PO平分∠BPD；

（2）PA=PC．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】

试题分析：（1）过点O作OE⊥AB，OF⊥CD，垂足分别为E、F，根据AB=CD可知OE=OF，进而可知PO平分∠BPD；

（2）先根据全等三角形的判定定理得出Rt△POE≌Rt△POF，再由垂径定理可得出AE=CF，再根据PE﹣AE=PF﹣CF即可得出结论．

试题解析：（1）过点O作OE⊥AB，OF⊥CD，垂足分别为E、F，

∵AB=CD，

∴OE=OF，

∴PO平分∠BPD；

（2）在Rt△POE与Rt△POF中，

∵OP=OP，OE=OF，

∴Rt△POE≌Rt△POF，

∴PE=PF，

∵AB=CD，OE⊥AB，OF⊥CD，E、F分别为垂足，

∴AE=AB，

CF=CD，

∴AE=CF，

∴PE﹣AE=PF﹣CF，即PA=PC．