题目内容
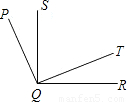
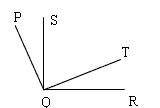
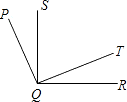 如图,∠PQR等于138°,SQ⊥QR,QT⊥PQ.则∠SQT等于
如图,∠PQR等于138°,SQ⊥QR,QT⊥PQ.则∠SQT等于
- A.42°
- B.64°
- C.48°
- D.24°
A
分析:利用垂直的概念和互余的性质计算.
解答:∵∠PQR等于138°,QT⊥PQ,
∴∠PQS=138°-90°=48°,
又∵SQ⊥QR,
∴∠PQT=90°,
∴∠SQT=42°.
故选A.
点评:本题是对有公共部分的两个直角的求角度的考查,注意直角的定义和度数.
分析:利用垂直的概念和互余的性质计算.
解答:∵∠PQR等于138°,QT⊥PQ,
∴∠PQS=138°-90°=48°,
又∵SQ⊥QR,
∴∠PQT=90°,
∴∠SQT=42°.
故选A.
点评:本题是对有公共部分的两个直角的求角度的考查,注意直角的定义和度数.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目