题目内容
设a、b、c和S分别为三角形的三边长和面积,关于x的方程b2x2+(b2+c2-a2)x+c2=0的判别式为Δ.则Δ与S的大小关系为( ).
| A.Δ=16S2 | B.Δ=-16S2 | C.Δ=16S | D.Δ=-16S |
B
试题分析:因为
Δ=(b2+c2-a2)2-4b2c2=(b2+c2-a2+2bc)(b2+c2-a2-2bc)
=[(b+c)2-a2][(b-c)2-a2]=(b+c+a)(b+c-a)(b-c+a)(b-c-a).
记p=
 (a+b+c),所以,Δ=2p·2(p-a)·2(p-c)[-2(p-b)]=-16p(p-a)(p-b)(p-c).
(a+b+c),所以,Δ=2p·2(p-a)·2(p-c)[-2(p-b)]=-16p(p-a)(p-b)(p-c).由海伦公式知S2=p(p-a)(p-b)(p-c).
故Δ=-16S2
点评:本题难度较大,主要考查学生对平方差公式知识点的掌握,设计海伦公式,最后代入取值即可。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,且
,且 ,则
,则 .
.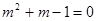 ,则
,则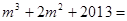 _______ .
_______ . 可分解为
可分解为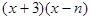 ,则m、n的值为( )
,则m、n的值为( )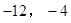

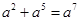
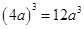
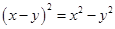
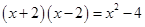
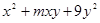 是一个完全平方式,则
是一个完全平方式,则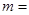 ( )
( )
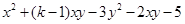 中不含xy项.
中不含xy项.