题目内容
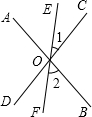
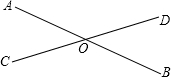
如图，直线AB、CD、EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD=24°，∠COG的度数=______．
∵AB⊥CD，
∴∠AOC=∠BOC=90°，
∵∠COE=∠FOD=24°，
∴∠AOE=∠AOC+∠COE=90°+24°=114°，
∵OG平分∠AOE，
∴∠GOE=
∠AOE=
×114°=57°，
∴∠COG=∠GOE-∠COE=57°-24°=33°．
故答案为：33°．
∴∠AOC=∠BOC=90°，
∵∠COE=∠FOD=24°，
∴∠AOE=∠AOC+∠COE=90°+24°=114°，
∵OG平分∠AOE，
∴∠GOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COG=∠GOE-∠COE=57°-24°=33°．
故答案为：33°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
