题目内容
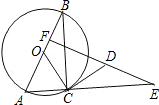 如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点,ED⊥AB于F.
如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点,ED⊥AB于F.(1)判断△DCE的形状;
(2)设⊙O的半径为1,且OF=
| ||
| 2 |
分析:(1)易得△AOC是正三角形,故有∠E=30°,由∠OCD=90°和平角的概念可得∠DCE=30°=∠E,所以DE=CD;进而可知此三角形为等腰三角形.
(2)由勾股定理求得BC=
,然后由直角三角形的性质,求得CE=
,即可证得△DCE≌△OCB.
(2)由勾股定理求得BC=
| 3 |
| 3 |
解答:(1)解:∵∠ABC=30°,
∴∠BAC=60°.
又∵OA=OC,
∴△AOC是正三角形.
又∵CD是切线,
∴∠OCD=90°.
∴∠DCE=180°-60°-90°=30°.
而ED⊥AB于F,
∴∠CED=90°-∠BAC=30°.
故△CDE为等腰三角形.
(2)证明:∵CD是⊙O的切线,
∴∠OCD=90°,
∵∠BAC=60°,AO=CO,
∴∠OCA=60°,∵∠DCE=30°.
∴A,C,E三点同线
在△ABC中,
∵AB=2,AC=AO=1,
∴BC=
=
.
∵OF=
,
∴AF=AO+OF=
.
又∵∠AEF=30°,
∴AE=2AF=
+1,
∴CE=AE-AC=
=BC,
而∠OCB=∠ACB-∠ACO=90°-60°=30°=∠ABC;
故△CDE≌△COB.
∴∠BAC=60°.
又∵OA=OC,
∴△AOC是正三角形.
又∵CD是切线,
∴∠OCD=90°.
∴∠DCE=180°-60°-90°=30°.
而ED⊥AB于F,
∴∠CED=90°-∠BAC=30°.
故△CDE为等腰三角形.
(2)证明:∵CD是⊙O的切线,
∴∠OCD=90°,
∵∠BAC=60°,AO=CO,
∴∠OCA=60°,∵∠DCE=30°.
∴A,C,E三点同线
在△ABC中,
∵AB=2,AC=AO=1,
∴BC=
| 22-12 |
| 3 |
∵OF=
| ||
| 2 |
∴AF=AO+OF=
| ||
| 2 |
又∵∠AEF=30°,
∴AE=2AF=
| 3 |
∴CE=AE-AC=
| 3 |
而∠OCB=∠ACB-∠ACO=90°-60°=30°=∠ABC;
故△CDE≌△COB.
点评:本题利用了直径对的圆周角是直角,等边三角形的判定和性质,勾股定理,切线的性质,直角三角形的性质求解.

练习册系列答案
相关题目
 7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( )
7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( ) 如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.
如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F. 24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长.
24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长. (2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB. 如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5
如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5