题目内容
【题目】在平面直角坐标系中![]() ,
,![]() 且满足
且满足![]() ,长方形
,长方形![]() 在坐标系中(如图),点
在坐标系中(如图),点![]() 为坐标系的原点.
为坐标系的原点.

(1)求点![]() 的坐标.
的坐标.
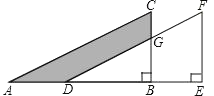
(2)如图1,若点![]() 从点
从点![]() 出发,以2个单位/秒的速度向右运动(不超过点
出发,以2个单位/秒的速度向右运动(不超过点![]() ),点
),点![]() 从原点
从原点![]() 出发,以1个单位/秒的速度向下运动(不超过点
出发,以1个单位/秒的速度向下运动(不超过点![]() ),设
),设![]() 、
、![]() 两点同时出发,在它们运动的过程中,四边形
两点同时出发,在它们运动的过程中,四边形![]() 的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,![]() 为
为![]() 轴负半轴上一点,且
轴负半轴上一点,且![]() ,
,![]() 是
是![]() 轴正半轴上一动点,
轴正半轴上一动点,![]() 的平分线
的平分线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在点
,在点![]() 运动的过程中,请探究
运动的过程中,请探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)B(6,3);(2)9;(3)∠CFE=2∠D,理由见解析;
【解析】
(1)根据题意可得a=6,c=3,则可求A点,C点,B点坐标;
(2)设M、N同时出发的时间为t,则S![]() =S
=S![]() S
S![]() S
S![]() =18
=18![]() ×2t×3
×2t×3![]() ×6×(3t)=9.与时间无关,即面积是定值,其值为9;
×6×(3t)=9.与时间无关,即面积是定值,其值为9;
(3)根据三角形内角和定理和三角形外角等于不相邻的两个内角的和,可求∠CFE与∠D的数量关系.
(1)∵![]() ,
,
∴a=6,c=3
∴A(6,0),C(0,3)
∵四边形OABC是矩形
∴AO∥BC,AB∥OC,AB=OC=3,AO=BC=6
∴B(6,3)
(2)四边形MBNO的面积不变.
设M、N同时出发的时间为t,
则S![]() =S
=S![]() S
S![]() S
S![]() =18
=18![]() ×2t×3
×2t×3![]() ×6×(3t)=9.与时间无关.
×6×(3t)=9.与时间无关.
∴在运动过程中面积不变,是定值9.
(3)∠CFE=2∠D.
理由如下:如图
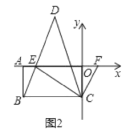
∵∠CBE=∠CEB
∴∠ECB=180°2∠BEC
∵CDP平分∠ECF
∴∠DCE=∠DCF
∵AF∥BC
∴∠F=180°∠DCF∠DCE∠BCE=180°2∠DCE(180°2∠BEC)
∴∠F=2∠BEC2∠DCE
∵∠BEC=∠D+∠DCE
∴∠F=2(∠D+∠DCE)2∠DCE
∴∠F=2∠D

【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?