��Ŀ����
�۲졢���롢̽����
�ڡ�ABC�У���ACB=2��B��
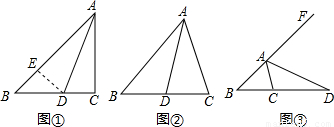
��1����ͼ�٣�����C=90�㣬ADΪ��BAC�Ľ�ƽ����ʱ����֤��AB=AC+CD��
��2����ͼ�ڣ�����C��90�㣬ADΪ��BAC�Ľ�ƽ����ʱ���߶�AB��AC��CD����������������ϵ������Ҫ֤������ֱ��д����IJ��룻
��3����ͼ�ۣ���ADΪ��ABC�����ƽ����ʱ���߶�AB��AC��CD����������������ϵ����д����IJ��룬������IJ������֤����

�ڡ�ABC�У���ACB=2��B��
��1����ͼ�٣�����C=90�㣬ADΪ��BAC�Ľ�ƽ����ʱ����֤��AB=AC+CD��
��2����ͼ�ڣ�����C��90�㣬ADΪ��BAC�Ľ�ƽ����ʱ���߶�AB��AC��CD����������������ϵ������Ҫ֤������ֱ��д����IJ��룻
��3����ͼ�ۣ���ADΪ��ABC�����ƽ����ʱ���߶�AB��AC��CD����������������ϵ����д����IJ��룬������IJ������֤����

��������1����D��DE��AB����AB�ڵ�E�����ɽ�ƽ�������ʵõ�ED=CD������HL�õ�ֱ��������AED��ֱ��������ACDȫ�ȣ���ȫ�������εĶ�Ӧ����ȣ���Ӧ����ȣ��õ�AE=AC����AED=��ACB���ɡ�ACB=2��B�����õ���������������ʵõ�һ�Խ���ȣ����õȽǶԵȱߵõ�BE=DE����AB=AE+EB�������������ɵ�֤��
��2��AB=CD+AC������Ϊ����AB�Ͻ�ȡAG=AC����ͼ2��ʾ���ɽ�ƽ���߶���õ�һ�Խ���ȣ�����AD=AD������SAS�õ�������AGD��������ACDȫ�ȣ�������ͬ��1�����ɵ�֤��
��3��AB=CD-AC������Ϊ����AF�Ͻ�ȡAG=AC����ͼ3��ʾ��ͬ��2�����ɵ�֤��
��2��AB=CD+AC������Ϊ����AB�Ͻ�ȡAG=AC����ͼ2��ʾ���ɽ�ƽ���߶���õ�һ�Խ���ȣ�����AD=AD������SAS�õ�������AGD��������ACDȫ�ȣ�������ͬ��1�����ɵ�֤��
��3��AB=CD-AC������Ϊ����AF�Ͻ�ȡAG=AC����ͼ3��ʾ��ͬ��2�����ɵ�֤��
���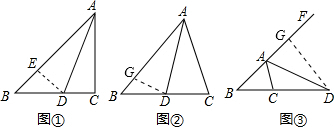
�⣺��1����D��DE��AB����AB�ڵ�E����ͼ1��ʾ��
��ADΪ��BAC��ƽ���ߣ�DC��AC��DE��AB��
��DE=DC��
��Rt��ACD��Rt��AED��
AD=AD��DE=DC��
��Rt��ACD��Rt��AED��HL����
��AC=AE����ACB=��AED��
�ߡ�ACB=2��B��
���AED=2��B��
�֡ߡ�AED=��B+��EDB��
���B=��EDB��
��BE=DE=DC��
��AB=BE+AE=CD+AC��
��2��AB=CD+AC��������
��AB�Ͻ�ȡAG=AC����ͼ2��ʾ��
��ADΪ��BAC��ƽ���ߣ�
���GAD=��CAD��
���ڡ�ADG�͡�ADC�У�
��
���ADG�ա�ADC��SAS����
��CD=CG����AGD=��ACB��
�ߡ�ACB=2��B��
���AGD=2��B��
�֡ߡ�AGD=��B+��GDB��
���B=��GDB��
��BE=DG=DC��
��AB=BG+AG=CD+AC��
��3��AB=CD-AC��������
��AF�Ͻ�ȡAG=AC����ͼ3��ʾ��
��ADΪ��FAC��ƽ���ߣ�
���GAD=��CAD��
���ڡ�ADG�͡�ACD�У�
��
���ADG�ա�ACD��SAS����
��CD=GD����AGD=��ACD������ACB=��FGD��
�ߡ�ACB=2��B��
���FGD=2��B��
�֡ߡ�FGD=��B+��GDB��
���B=��GDB��
��BG=DG=DC��
��AB=BG-AG=CD-AC��

�⣺��1����D��DE��AB����AB�ڵ�E����ͼ1��ʾ��
��ADΪ��BAC��ƽ���ߣ�DC��AC��DE��AB��
��DE=DC��
��Rt��ACD��Rt��AED��
AD=AD��DE=DC��
��Rt��ACD��Rt��AED��HL����
��AC=AE����ACB=��AED��
�ߡ�ACB=2��B��
���AED=2��B��
�֡ߡ�AED=��B+��EDB��
���B=��EDB��
��BE=DE=DC��
��AB=BE+AE=CD+AC��
��2��AB=CD+AC��������
��AB�Ͻ�ȡAG=AC����ͼ2��ʾ��
��ADΪ��BAC��ƽ���ߣ�
���GAD=��CAD��
���ڡ�ADG�͡�ADC�У�
|
���ADG�ա�ADC��SAS����
��CD=CG����AGD=��ACB��
�ߡ�ACB=2��B��
���AGD=2��B��
�֡ߡ�AGD=��B+��GDB��
���B=��GDB��
��BE=DG=DC��
��AB=BG+AG=CD+AC��
��3��AB=CD-AC��������
��AF�Ͻ�ȡAG=AC����ͼ3��ʾ��
��ADΪ��FAC��ƽ���ߣ�
���GAD=��CAD��
���ڡ�ADG�͡�ACD�У�
|
���ADG�ա�ACD��SAS����
��CD=GD����AGD=��ACD������ACB=��FGD��
�ߡ�ACB=2��B��
���FGD=2��B��
�֡ߡ�FGD=��B+��GDB��
���B=��GDB��
��BG=DG=DC��
��AB=BG-AG=CD-AC��
���������⿼���˽�ƽ�������ʣ��Լ�ȫ�������ε��ж������ʣ��������ս�ƽ���������ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ