题目内容
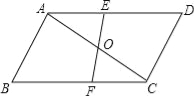
【题目】如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1
B.2
C.3
D.4
【答案】D
【解析】
试题分析:由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,据此对各结论进行判断.
△ABC与△CDA关于点O对称,则AB=CD、AD=BC,所以四边形ABCD是平行四边形,即点O就是ABCD的对称中心,则有:(1)点E和点F,B和D是关于中心O的对称点,正确;(2)直线BD必经过点O,正确;(3)四边形DEOC与四边形BFOA的面积必相等,正确;(5)△AOE与△COF成中心对称,正确;
其中正确的个数为4个

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目