题目内容
【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地，快车比慢车晚出发0.5小时，行驶一段时间后，快车途中体息，休息后继续按原速行驶，到达乙地后停止．慢车和快车离甲地的距离y（千米）与慢车行驶时间x（小时）之间的函数关系如图所示．
（1）直接写出快车速度是 千米/小时．
（2）求快车到达乙地比慢车到达乙地早了多少小时？
（3）求线段BC对应的函数关系式．
【答案】（1）120；（2）快车到达乙地比慢车到达乙地早了0.5小时；（3）y＝120x﹣60．
【解析】
（1）根据速度＝路程÷时间即可求出快车的速度；
（2）先求出慢车到达乙地的时间，再减去快车到达乙地的时间即可求解；
（3）得出B、C的坐标利用待定系数法解答即可．
解：（1）快车速度是（400﹣280）÷（4.5﹣3.5）＝120（千米/小时）．
故答案为：120；
（2）∵慢车速度是280÷3.5＝80（千米/小时）．
∴慢车到达乙地需要的时间是400÷80＝5（小时），
∴快车到达乙地比慢车到达乙地早了5﹣4.5＝0.5（小时）；
（3）∵快车比慢车晚出发0.5小时，
∴B的坐标为（0.5，0），
∵快车从甲地驶向乙地需要的时间是400÷120＝
（小时）；
又实际到达时间是慢车出发后4.5小时，且快车比慢车晚出发0.5小时，
∴快车途中休息时间是4.5﹣0.5﹣＝
（小时）
2﹣
，
∵
，
∴点C的坐标为（
，100），
设BC的解析式为：y＝kx+b，
把B（0.5，0）和C（，100）代入解析式可得：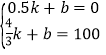
，
解得：
，
所以BC的解析式为：y＝120x﹣60．
新思维假期作业寒假吉林大学出版社系列答案
【题目】现在电器进入销售旺季，福清某电器超市销售每台进价分别为
元、
元的
两种型号的电器，下表是近两周的销售情况：（进价、售价均保持不变，利润=销售收入-进货成本）
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
（1）求两种型号的电器销售单价；
（2）若超市准备用不超过
元的金额再采购这种型号的电器共台，销售完这台电器实现利润超过
元的目标，请给出相应的采购方案；并求出利润的最大值.
