题目内容
计算:(1)2t-4=3t+5
(2)4-3(x-3)=x+10
(3)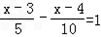
(4)
(5)设 ,当x为何值时,y1与y2互为相反数?
,当x为何值时,y1与y2互为相反数?
(2)4-3(x-3)=x+10
(3)
(4)

(5)设
 ,当x为何值时,y1与y2互为相反数?
,当x为何值时,y1与y2互为相反数?解:(1)移项得:2t-3t=5+4;
合并同类项得:-t=9,
系数化1得:t=-9;
(2)去括号得:4-3x+9=x+10,
移项得:-3x-x=10-4-9,
合并同类项得:-4x=-3,
系数化1得:x= ;
;
(3)去分母得:2x-6-x+4=10,
合并同类项得:x=12;
(4)去分母得:0.005x﹣0.15﹣0.002x﹣0.02=0.04,
移项合并同类项得:0.003x=0.75,
系数化1得:x=250;
(5)据题意可列方程: x+1+
x+1+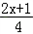 =0,
=0,
去分母得:4x+20+10x+5=0,
移项合并同类项得:14x=﹣25,
系数化1得:x=﹣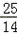 .
.
合并同类项得:-t=9,
系数化1得:t=-9;
(2)去括号得:4-3x+9=x+10,
移项得:-3x-x=10-4-9,
合并同类项得:-4x=-3,
系数化1得:x=
 ;
;(3)去分母得:2x-6-x+4=10,
合并同类项得:x=12;
(4)去分母得:0.005x﹣0.15﹣0.002x﹣0.02=0.04,
移项合并同类项得:0.003x=0.75,
系数化1得:x=250;
(5)据题意可列方程:
 x+1+
x+1+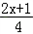 =0,
=0,去分母得:4x+20+10x+5=0,
移项合并同类项得:14x=﹣25,
系数化1得:x=﹣
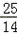 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目