题目内容
【题目】如图![]() 是
是![]() 的中线,
的中线,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
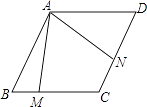
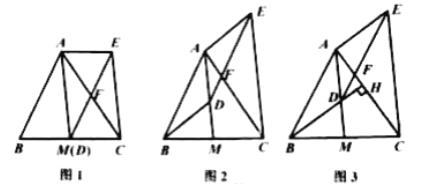
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
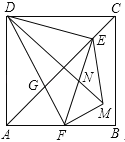
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .当
.当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)结论成立,理由详见解析;(3)DH=1+![]() .
.
【解析】
试题分析:(1)由DE//AB,可得同位角相等:∠EDC=∠ABM,由CE//AM,可得同位角相等∠ECD=∠ADB,又由BD=DC,则△ABD△EDC,得到AB=ED,根据有一组对边平行且相等,可得四边形ABDE为平行四边形.(2)过点M作MG//DE交EC于点G,则可得四边形DMGE为平行四边形,且ED=GM且ED//GM,由(1)可得AB=GM且AB//GM,即可证得;(3)在已知条件中没有已知角的度数时,则在求角度时往特殊角30°,60°,45°的方向考虑,则要求这样的特殊角,就去找边的关系,构造直角三角形,取线段HC的中点I,连结MI,则MI是△BHC的中位线,可得MI//BH,MI=![]() BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;设DH=x,即可用x分别表示出AH=
BH,且MI⊥AC,则去找Rt△AMI中边的关系,求出∠CAM;设DH=x,即可用x分别表示出AH=![]() x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可.
x,AD=2x,AM=4+2x,BH=4+2x,由△HDF~△HBA,得到对应边成比例,求出x的值即可.
试题解析:(1)证明:∵DE//AB,∴∠EDC=∠ABM,
∵CE//AM,
∴∠ECD=∠ADB,
又∵AM是△ABC的中线,且D与M重合,∴BD=DC,
∴△ABD△EDC,
∴AB=ED,又∵AB//ED,
∴四边形ABDE为平行四边形。
(2)解:结论成立,理由如下:
过点M作MG//DE交EC于点G,
∵CE//AM,
∴四边形DMGE为平行四边形,
∴ED=GM且ED//GM,
由(1)可得AB=GM且AB//GM,
∴AB=ED且AB//ED.
∴四边形ABDE为平行四边形.
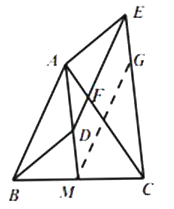
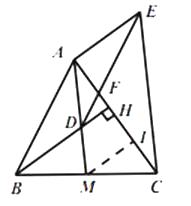
(3)
解:取线段HC的中点I,连结MI,
∴MI是△BHC的中位线,
∴MI//BH,MI=![]() BH,
BH,
又∵BH⊥AC,且BH=AM,
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°
设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,∴BH=4+2x,
由(2)已证四边形ABDE为平行四边形,
∴FD//AB,
∴△HDF~△HBA,
∴![]() , 即
, 即![]()
解得x=1±![]() (负根不合题意,舍去)
(负根不合题意,舍去)
∴DH=1+![]() .
.

 名校课堂系列答案
名校课堂系列答案