ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ ΐ―ßΩΈ…œΘ§Ν÷άœ ΠΗχ≥ωΝΥœ¬Ν–ΖΫΩρ÷–ΒΡ“ΜΒάΧβΘΚ
–Γ¥œΚΆΆ§Ήά–ΓΟςΧ÷¬έΚσΘ§ΒΟ≥ω»γœ¬Ϋβ¥πΘΚ
Θ®![]() Θ©ΧΊ β«ιΩωΘ§ΧΫΥςΫα¬έ
Θ©ΧΊ β«ιΩωΘ§ΧΫΥςΫα¬έ
Β±Βψ![]() ΈΣ
ΈΣ![]() ΒΡ÷–Βψ ±Θ§»γΆΦ
ΒΡ÷–Βψ ±Θ§»γΆΦ![]() Θ§»ΖΕ®œΏΕΈ
Θ§»ΖΕ®œΏΕΈ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘ§«κΡψ÷±Ϋ”–¥≥ωΫα¬έΘΚ
ΒΡ¥σ–ΓΙΊœΒΘ§«κΡψ÷±Ϋ”–¥≥ωΫα¬έΘΚ ![]() ______
______ ![]() Θ®ΧνΓΑ
Θ®ΧνΓΑ![]() Γ±ΓΑ
Γ±ΓΑ ![]() Γ±ΜρΓΑ
Γ±ΜρΓΑ![]() Γ±Θ©Θ°
Γ±Θ©Θ°
Θ®![]() Θ©ΧΊάΐΤτΖΔΘ§Ϋβ¥πΈ Χβ
Θ©ΧΊάΐΤτΖΔΘ§Ϋβ¥πΈ Χβ
ΫβΘΚΧβΡΩ÷–Θ§ ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒ «
ΒΡ¥σ–ΓΙΊœΒ «![]() __________
__________ ![]() Θ®ΧνΓΑ
Θ®ΧνΓΑ![]() Γ±ΓΑ
Γ±ΓΑ ![]() Γ±ΜρΓΑ
Γ±ΜρΓΑ![]() Γ±Θ©Θ§άμ”…»γœ¬ΘΚ»γΆΦ
Γ±Θ©Θ§άμ”…»γœ¬ΘΚ»γΆΦ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Θ®«κΡψΦΧ–χΆξ≥…Ϋ”œ¬ά¥ΒΡΫβΧβΙΐ≥ΧΘ©Θ°
Θ§Θ®«κΡψΦΧ–χΆξ≥…Ϋ”œ¬ά¥ΒΡΫβΧβΙΐ≥ΧΘ©Θ°
Θ®![]() Θ©ΆΊ’ΙΧ÷¬έΘ§…ηΦΤ–¬Χβ
Θ©ΆΊ’ΙΧ÷¬έΘ§…ηΦΤ–¬Χβ
ΔΌΜΞΜΜΝ÷άœ ΠΥυΗχΧβΒΡΧθΦΰΚΆΫα¬έΘ§Φ¥ΘΚ»γΆΦ![]() ‘ΎΒ»±Ώ»ΐΫ«–Έ
‘ΎΒ»±Ώ»ΐΫ«–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œΘ§«“
ΒΡ―”≥ΛœΏ…œΘ§«“![]() Θ§ ‘»ΖΕ®œΏΕΈ
Θ§ ‘»ΖΕ®œΏΕΈ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΔΎ‘ΎΒ»±Ώ»ΐΫ«–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ§«“
…œΘ§«“![]() Θ§»τ
Θ§»τ![]() ΒΡ±Ώ≥ΛΈΣ
ΒΡ±Ώ≥ΛΈΣ![]() Θ§
Θ§ ![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΈΣ__________Θ®«κΡψ÷±Ϋ”–¥≥ωΫαΙϊΘ©Θ°
ΒΡ≥ΛΈΣ__________Θ®«κΡψ÷±Ϋ”–¥≥ωΫαΙϊΘ©Θ°
»γΆΦΘ§‘ΎΒ»±Ώ»ΐΫ«–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘Ύ
‘Ύ![]()
…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œΘ§«“
ΒΡ―”≥ΛœΏ…œΘ§«“![]() Θ§
Θ§
‘»ΖΕ®œΏΕΈ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®![]() Θ©
Θ©![]() ΘΜΘ®
ΘΜΘ®![]() Θ©
Θ©![]() Θ§ΦϊΫβΈωΘΜΘ®
Θ§ΦϊΫβΈωΘΜΘ®![]() Θ©ΔΌ
Θ©ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() Μρ
Μρ![]() Θ°
Θ°
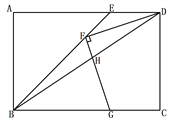
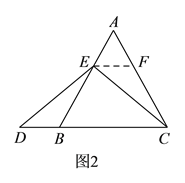
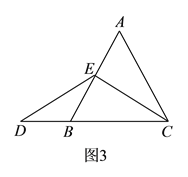
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§ΒψEΈΣABΒΡ÷–ΒψΘ§Φ¥Ω…ΒΟ≥ωCEΓΆABΘ§ΫχΕχΒΟ≥ωΓœECD=ΓœDΘ§Φ¥Ω…ΒΟ≥ωœΏΕΈED”κECΒΡ¥σ–ΓΙΊœΒΘΜ
Θ®2Θ© Ήœ»ΒΟ≥ωBE=CFΘ§ΫχΕχάϊ”ΟΓςDBEΓ’ΓςEFCΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Θ®3Θ©ΔΌΉς![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ω…÷Σ
Θ§Ω…÷Σ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΫχΕχ÷ΛΟς
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΫχΕχ÷ΛΟς![]() Γ’
Γ’![]() Θ§Φ¥Ω…ΒΟ≥ω
Θ§Φ¥Ω…ΒΟ≥ω![]() ΘΜ
ΘΜ
ΔΎΖ÷ΒψD‘ΎCBΒΡ―”≥ΛœΏ…œΓΔ‘ΎBCΒΡ―”≥ΛœΏ…œΝΫ÷÷«ιΩωΫχ––Χ÷¬έΦ¥Ω…ΒΟ.
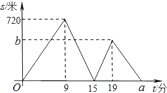
‘ΧβΫβΈωΘΚΘ®![]() Θ©
Θ©![]() Θ°
Θ°
ΓΏ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ ![]() «
«![]() ÷–ΒψΘ§Γύ
÷–ΒψΘ§Γύ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ°
Θ°
ΓΏ![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ°
Θ°
Θ®![]() Θ©
Θ©![]()
‘ΎΒ»±Ώ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
Γύ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
Γύ![]() Θ§
Θ§
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Ά§άμ![]() Θ§
Θ§
”÷‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
‘Ύ![]() ΚΆ
ΚΆ![]() ÷–Θ§
÷–Θ§
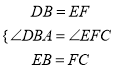 Θ§
Θ§
Γύ![]() Γ’
Γ’![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
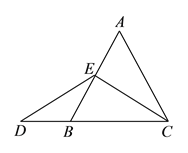
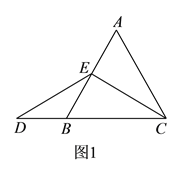
Θ®![]() Θ©ΔΌΉς
Θ©ΔΌΉς![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§
‘ρΩ…÷Σ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
Γύ![]() Θ°
Θ°
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏ‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() ΚΆ
ΚΆ![]() ÷–Θ§
÷–Θ§
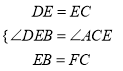 Θ§
Θ§
Γύ![]() Γ’
Γ’![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
ΔΎ![]() Θ§
Θ§
Γύ![]() Μρ
Μρ![]() Θ°
Θ°