题目内容
(2012•东莞)有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y).
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式
+
有意义的(x,y)出现的概率;
(3)化简分式
+
,并求使分式的值为整数的(x,y)出现的概率.
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式
| x2-3xy |
| x2-y2 |
| y |
| x-y |
(3)化简分式
| x2-3xy |
| x2-y2 |
| y |
| x-y |
分析:(1)根据题意列出图表,即可表示(x,y)所有可能出现的结果;
(2)根据(1)中的树状图求出使分式
+
有意义的情况,再除以所有情况数即可;
(3)先化简,再找出使分式的值为整数的(x,y)的情况,再除以所有情况数即可.
(2)根据(1)中的树状图求出使分式
| x2-3xy |
| x2-y2 |
| y |
| x-y |
(3)先化简,再找出使分式的值为整数的(x,y)的情况,再除以所有情况数即可.
解答:解:(1)用列表法表示(x,y)所有可能出现的结果如下:
(2)∵使分式
+
有意义的(x,y)有(-1,-2)、(1,-2)、(-2,-1)、(-2,1)4种情况,
∴使分式
+
有意义的(x,y)出现的概率是
,
(3)∵
+
=
(x≠±y),
使分式的值为整数的(x,y)有(1,-2)、(-2,1)2种情况,
∴使分式的值为整数的(x,y)出现的概率是
.
| -2 | -1 | 1 | |
| -2 | (-2,-2) | (-1,-2) | (1,-2) |
| -1 | (-2,-1) | (-1,-1) | (1,-1) |
| 1 | (-2,1) | (-1,1) | (1,1) |
| x2-3xy |
| x2-y2 |
| y |
| x-y |
∴使分式
| x2-3xy |
| x2-y2 |
| y |
| x-y |
| 4 |
| 9 |
(3)∵
| x2-3xy |
| x2-y2 |
| y |
| x-y |
| x-y |
| x+y |
使分式的值为整数的(x,y)有(1,-2)、(-2,1)2种情况,
∴使分式的值为整数的(x,y)出现的概率是
| 2 |
| 9 |
点评:此题考查了树状图法与列表法求概率.此题难度不大,解题的关键是根据题意画出树状图或列出表格,注意树状图法与列表法可以不重不漏地表示出所有等可能的结果,注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
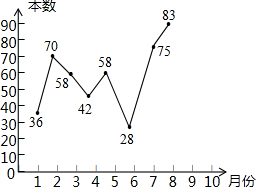 (2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
(2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( ) 写出数字1,2,3,4,5,6,7,….
写出数字1,2,3,4,5,6,7,….