题目内容
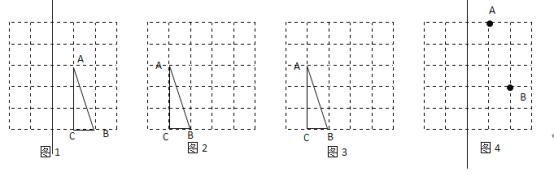
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
【答案】(1)图见解析;(2)图见解析;(3)图见解析;(4)图见解析
【解析】
(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 即可;
即可;
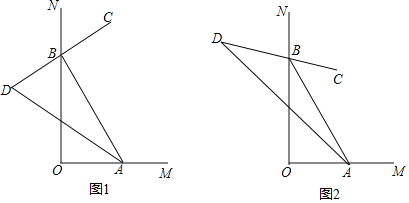
(2)如解图2,连接CH,交AB于点D,利用SAS证出△ACB≌△CGH,从而得出∠BAC=∠HCG,然后利用等量代换即可求出∠CDB=90°;
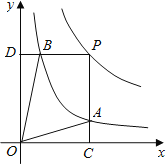
(3)如解图3,连接CP交AB于点E,利用矩形的性质可得AE=BE;
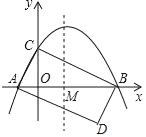
(4)如解图4,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM,根据平行四边形的性质和两点之间线段最短即可推出此时MN即为所求.
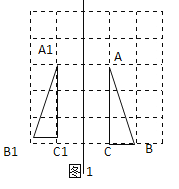
解:(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,如图1所示,
,如图1所示,![]() 即为所求;
即为所求;
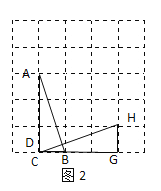
(2)如图2所示连接CH,交AB于点D,
在△ACB和△CGH中
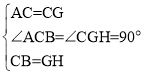
∴△ACB≌△CGH
∴∠BAC=∠HCG
∵∠BAC+∠ABC=90°
∴∠HCG+∠ABC=90°
∴∠CDB=90°
∴CD为△ABC的高,故CD即为所求;
(3)如图3所示,连接CP交AB于点E
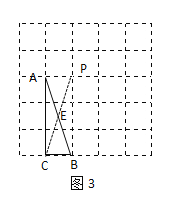
由图可知:四边形ACBP为矩形
∴AE=EB
∴CE为△ABC的中线,故CE即为所求;
(4)如图4所示,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM
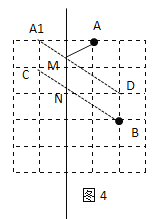
根据对称性可知:AM=A1M
由图可知:A1C=BD=1个单位长度,A1C∥BD∥直线l
∴四边形A1CBD为平行四边形
∴A1D∥BC
∴四边形A1CNM和四边形MNBD均为平行四边形
∴A1M=CN,MN=BD=1个单位长度
∴AM=CN
∴AM+NB=CN+NB=CB,
根据两点之间线段最短,此时AM+NB最小,而MN=1个单位长度为固定值,
∴此时![]() 最小,故此时MN即为所求.
最小,故此时MN即为所求.

 优生乐园系列答案
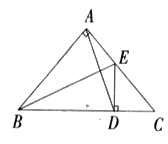
优生乐园系列答案【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下4个结论:①
的中点.以下4个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() 以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
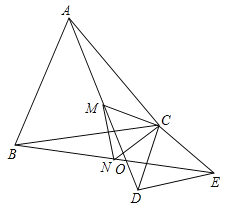
【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量(吨) | 10 | 6 | 4 |
每吨土特产利润(万元) | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.