题目内容
13.已知⊙O的直径AB=10cm,弦CD⊥AB于点M.若OM:OA=3:5,则弦AC的长为多少?分析 根据题意画出图形,求得Cm=4cm,则AM的长,由勾股定理得AC的长.
解答 
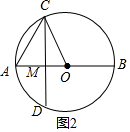 解:如图1,∵AB=10cm,弦CD⊥AB于点M.若OM:OA=3:5,
解:如图1,∵AB=10cm,弦CD⊥AB于点M.若OM:OA=3:5,
∴OA=OC=5,OM=3,AM=8,
∴CM=$\sqrt{O{C}^{2}-O{M}^{2}}$=4,
∴AC=$\sqrt{C{M}^{2}+A{M}^{2}}$=4$\sqrt{5}$,
如图2,∵AB=10cm,弦CD⊥AB于点M.若OM:OA=3:5,
∴OA=OC=5,OM=3,AM=2,
∴CM=$\sqrt{O{C}^{2}-O{M}^{2}}$=4,
∴AC=$\sqrt{C{M}^{2}+A{M}^{2}}$=2$\sqrt{5}$,
综上所述:弦AC的长为4$\sqrt{5}$cm或2$\sqrt{5}$cm.
点评 本题考查了勾股定理,垂径定理.解此类题目要注意将圆的问题转化成三角形的问题再进行计算.

练习册系列答案
相关题目
1.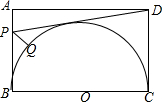 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )| A. | 5 | B. | $\sqrt{13}$+2 | C. | $\frac{\sqrt{73}}{2}$+$\frac{1}{2}$ | D. | 3$\sqrt{5}$-2 |
 如图,已知在?ABCD中,AE平分∠BAD,即∠1=∠2,BF平分∠ABC,即∠3=∠4,连接EF,求证:四边形ABEF是菱形.
如图,已知在?ABCD中,AE平分∠BAD,即∠1=∠2,BF平分∠ABC,即∠3=∠4,连接EF,求证:四边形ABEF是菱形. 如图弓形中,AB=30$\sqrt{3}$,弓高h为15,求:
如图弓形中,AB=30$\sqrt{3}$,弓高h为15,求: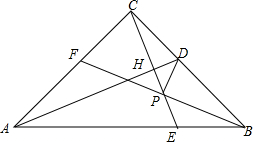 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( )
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( )