题目内容
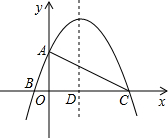 (2013•涉县模拟)如图,已知二次函数y=-
(2013•涉县模拟)如图,已知二次函数y=-| 1 |
| 4 |
| 3 |
| 2 |
(1)点A的坐标为
(0,4)
(0,4)
,点C的坐标为(8,0)
(8,0)
;(2)△ABC是直角三角形吗?若是,请给予证明;
(3)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由.
分析:(1)抛物线的解析式中,令x=0即得二次函数与y轴交点A的纵坐标,令y=0即得二次函数与x轴交点的横坐标.
(2)根据(1)中点的坐标得出AB,BC,AC的长,进而利用勾股定理逆定理得出即可;
(3)根据A、C的坐标,易求得直线AC的解析式,由于等腰△EDC的腰和底不确定,因此要分成三种情况讨论:
①CD=DE,由于OD=3,DA=DC=5,此时A点符合E点的要求,即此时A、E重合;
②CE=DE,根据等腰三角形三线合一的性质知:E点横坐标为点D的横坐标加上CD的一半,然后将其代入直线AC的解析式中,即可得到点E的坐标;
③CD=CE,此时CE=5,过E作EG⊥x轴于G,已求得CE、CA的长,即可通过相似三角形(△CEG∽△CAO)所得比例线段求得EG、CG的长,从而得到点E的坐标.
(2)根据(1)中点的坐标得出AB,BC,AC的长,进而利用勾股定理逆定理得出即可;
(3)根据A、C的坐标,易求得直线AC的解析式,由于等腰△EDC的腰和底不确定,因此要分成三种情况讨论:
①CD=DE,由于OD=3,DA=DC=5,此时A点符合E点的要求,即此时A、E重合;
②CE=DE,根据等腰三角形三线合一的性质知:E点横坐标为点D的横坐标加上CD的一半,然后将其代入直线AC的解析式中,即可得到点E的坐标;
③CD=CE,此时CE=5,过E作EG⊥x轴于G,已求得CE、CA的长,即可通过相似三角形(△CEG∽△CAO)所得比例线段求得EG、CG的长,从而得到点E的坐标.
解答:解:(1)在二次函数中令x=0得y=4,
∴点A的坐标为(0,4),
令y=0得:-
x2+
x+4=0,
即:x2-6x-16=0,
∴x=-2和x=8,
∴点B的坐标为(-2,0),点C的坐标为(8,0).
故答案为:A(0,4),C(8,0);
(2)∵点A的坐标为(0,4),
∴AO=4,
∵点B的坐标为(-2,0),点C的坐标为(8,0),
∴BO=2,CO=8,∴BC=10,
∴AC=
=4
,
∴AB=
=2
,
∴AB2+AC2=100,
∵BC2=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
(3)易得D(3,0),CD=5,
设直线AC对应的函数关系式为y=kx+b,则:
,
解得
;
∴y=-
x+4;
①当DE=DC时,
∵CD=5,
∴AD=5,
∵D(3,0),
∴OE=
=4,
 ∴E1(0,4);
∴E1(0,4);
②当DE=EC时,可得出E点在CD的垂直平分线上,可得出E点横坐标为:3+
=
,
进而将x=
代入y=-
x+4,得出y=
,
可得E2(
,
);
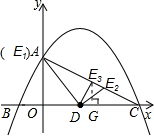
③当DC=EC时,如图,过点E作EG⊥CD,
则△CEG∽△CAO,
∴
=
=
,
即EG=
,CG=2
,
∴E3(8-2
,
);
综上所述,符合条件的E点共有三个:E1(0,4)、E2(
,
)、E3(8-2
,
).
∴点A的坐标为(0,4),
令y=0得:-
| 1 |
| 4 |
| 3 |
| 2 |
即:x2-6x-16=0,
∴x=-2和x=8,
∴点B的坐标为(-2,0),点C的坐标为(8,0).
故答案为:A(0,4),C(8,0);
(2)∵点A的坐标为(0,4),
∴AO=4,
∵点B的坐标为(-2,0),点C的坐标为(8,0),
∴BO=2,CO=8,∴BC=10,
∴AC=
| 42+82 |
| 5 |
∴AB=
| 22+42 |
| 5 |
∴AB2+AC2=100,
∵BC2=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
(3)易得D(3,0),CD=5,
设直线AC对应的函数关系式为y=kx+b,则:
|
解得
|
∴y=-
| 1 |
| 2 |
①当DE=DC时,
∵CD=5,
∴AD=5,
∵D(3,0),
∴OE=
| 52-32 |
 ∴E1(0,4);
∴E1(0,4);②当DE=EC时,可得出E点在CD的垂直平分线上,可得出E点横坐标为:3+
| 5 |
| 2 |
| 11 |
| 2 |
进而将x=
| 11 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
可得E2(
| 11 |
| 2 |
| 5 |
| 4 |
③当DC=EC时,如图,过点E作EG⊥CD,
则△CEG∽△CAO,
∴
| EG |
| OA |
| CG |
| OC |
| CE |
| AC |
即EG=
| 5 |
| 5 |
∴E3(8-2
| 5 |
| 5 |
综上所述,符合条件的E点共有三个:E1(0,4)、E2(
| 11 |
| 2 |
| 5 |
| 4 |
| 5 |
| 5 |
点评:此题考查了二次函数图象与坐标轴交点坐标的求法、等腰三角形的构成条件、图形面积的求法等知识,(3)题的解题过程并不复杂,关键在于理解题意.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
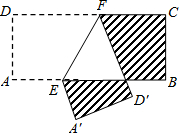 (2013•涉县模拟)如图,在矩形ABCD,AB=10cm,BC=5cm.点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A′、D′处,则整个阴影部分图形的周长为
(2013•涉县模拟)如图,在矩形ABCD,AB=10cm,BC=5cm.点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A′、D′处,则整个阴影部分图形的周长为