题目内容
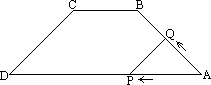
如图，在等腰梯形ABCD中，AB∥DC，AB=998，DC=1001，AD=1999，点P在线段AD上，则满足条件∠BPC=90°的点P的个数为
- A.0
- B.1
- C.2
- D.不小于3的整数
C
分析：要想求得点P的个数，由∠BPC=90°可判断以BC为直径的圆与AD的交点个数即可．
解答：AD的中点M对BC张成90°角，又在AD上取点N使AN=998，则ND=1001．由△ABN和△DCN都为等腰三角形推知∠BNC=90°，注意到以BC为直径的圆与AD至多有两个交点，可知所求点的个数为2．
点评：本题考查了圆周角定理、等腰梯形的性质以及直线与圆的位置关系：
①当圆心到直线的距离d＞圆的半径r，直线与圆相离；
②当圆心到直线的距离d＜圆的半径r，直线与圆相交；
③当圆心到直线的距离d=圆的半径r，直线与圆相切．
分析：要想求得点P的个数，由∠BPC=90°可判断以BC为直径的圆与AD的交点个数即可．
解答：AD的中点M对BC张成90°角，又在AD上取点N使AN=998，则ND=1001．由△ABN和△DCN都为等腰三角形推知∠BNC=90°，注意到以BC为直径的圆与AD至多有两个交点，可知所求点的个数为2．
点评：本题考查了圆周角定理、等腰梯形的性质以及直线与圆的位置关系：
①当圆心到直线的距离d＞圆的半径r，直线与圆相离；
②当圆心到直线的距离d＜圆的半径r，直线与圆相交；
③当圆心到直线的距离d=圆的半径r，直线与圆相切．
练习册系列答案
相关题目
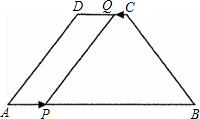在，求出这样的t的值；若不存在，请说明理由．
10、如图，在等腰梯形ABCD中，AD∥BC，AB=DC，E为AD的中点，求证：BE=CE．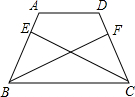
已知：如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点E、F分别在AB、DC上，且BE=3EA，CF=3FD．
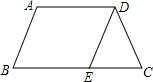（2012•广州）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC于点E，且EC=3，则梯形ABCD的周长是（ ）
