题目内容
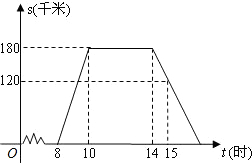 “五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
“五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
(1)小明全家在旅游景点游玩了多少小时?
(2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油 升.请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
升.请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
解:(1)由图象可知,小明全家在旅游景点游玩了4小时;
(2)设s=kt+b,由(14,180)及(15,120)
得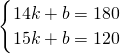 ,解得
,解得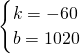
∴s=-60t+1020(14≤t≤17)
令s=0,得t=17.
答:返程途中s与时间t的函数关系是s=-60t+1020,
小明全家当天17:00到家;
(3)答案不唯一,大致的方案为:
①9:30前必须加一次油;
②若8:30前将油箱加满,则当天在油用完前的适当时间必须第二次加油;
③全程可多次加油,但加油总量至少为25升.
分析:(1)由图可知:10-14小时的时间段内小明全家在旅游景点游玩,因此时间应该是4小时;
(2)可根据14小时和15小时两个时间点的数值,用待定系数法求出函数的关系式;
(3)可根据8小时和10小时两个时间段的数值求出函数关系式,那么这个函数关系式应该是s=90x-720,那么出发时的15升油,可行驶的路程是15÷ =135千米,代入函数式中可得出x=9.5,因此9:30以前必须加一次油,如果刚出发就加满油,那么可行驶的路程=35÷
=135千米,代入函数式中可得出x=9.5,因此9:30以前必须加一次油,如果刚出发就加满油,那么可行驶的路程=35÷ =315千米>180千米,因此如果刚出发就加满油,到景点之前就不用再加油了.也可以多次加油,但要注意的是不要超出油箱的容量.
=315千米>180千米,因此如果刚出发就加满油,到景点之前就不用再加油了.也可以多次加油,但要注意的是不要超出油箱的容量.
点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.注意自变量的取值范围不能遗漏.
(2)设s=kt+b,由(14,180)及(15,120)
得
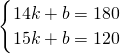 ,解得
,解得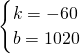
∴s=-60t+1020(14≤t≤17)
令s=0,得t=17.
答:返程途中s与时间t的函数关系是s=-60t+1020,
小明全家当天17:00到家;
(3)答案不唯一,大致的方案为:
①9:30前必须加一次油;
②若8:30前将油箱加满,则当天在油用完前的适当时间必须第二次加油;
③全程可多次加油,但加油总量至少为25升.
分析:(1)由图可知:10-14小时的时间段内小明全家在旅游景点游玩,因此时间应该是4小时;
(2)可根据14小时和15小时两个时间点的数值,用待定系数法求出函数的关系式;
(3)可根据8小时和10小时两个时间段的数值求出函数关系式,那么这个函数关系式应该是s=90x-720,那么出发时的15升油,可行驶的路程是15÷
 =135千米,代入函数式中可得出x=9.5,因此9:30以前必须加一次油,如果刚出发就加满油,那么可行驶的路程=35÷
=135千米,代入函数式中可得出x=9.5,因此9:30以前必须加一次油,如果刚出发就加满油,那么可行驶的路程=35÷ =315千米>180千米,因此如果刚出发就加满油,到景点之前就不用再加油了.也可以多次加油,但要注意的是不要超出油箱的容量.
=315千米>180千米,因此如果刚出发就加满油,到景点之前就不用再加油了.也可以多次加油,但要注意的是不要超出油箱的容量.点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.注意自变量的取值范围不能遗漏.

练习册系列答案
相关题目