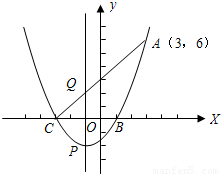题目内容
如图,一元二次方程x2+2x-3=0的两根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交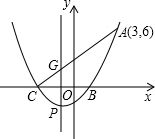 点C,B的横坐标,且此抛物线过点A(3,6).
点C,B的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点G,则P点坐标为
(3)在x轴上有一动点M,当MG+MA取得最小值时,求点M的坐标.
分析:(1)可先根据一元二次方程求出x1,x2的坐标,也就求出了B,C两点的坐标,然后可用交点式的二次函数通式来设二次函数的解析式,根据已知的A点的坐标求出二次函数的解析式.
(2)根据(1)二次函数解析式可得出顶点P的坐标和对称轴的解析式,G点就是直线AC与抛物线对称轴的交点,可先根据A,C的坐标,用待定系数法求出AC所在直线的解析式,然后将P点的横坐标代入求得的一次函数的解析式中即可求出G的坐标.
(3)本题的关键是先确定M点的位置,可先做A关于x轴的对称点A′然后连接A′C,与x轴的交点就是点M,那么可根据A′,C两点的坐标求出A′C所在直线的解析式,又已知了M在x轴上即可求出M点的坐标.
(2)根据(1)二次函数解析式可得出顶点P的坐标和对称轴的解析式,G点就是直线AC与抛物线对称轴的交点,可先根据A,C的坐标,用待定系数法求出AC所在直线的解析式,然后将P点的横坐标代入求得的一次函数的解析式中即可求出G的坐标.
(3)本题的关键是先确定M点的位置,可先做A关于x轴的对称点A′然后连接A′C,与x轴的交点就是点M,那么可根据A′,C两点的坐标求出A′C所在直线的解析式,又已知了M在x轴上即可求出M点的坐标.
解答:解:(1)解方程x2+2x-3=0
得x1=-3,x2=1.
∴抛物线与x轴的两个交点坐标为:C(-3,0),B(1,0),
设抛物线的解析式为y=a(x+3)(x-1).
∵A(3,6)在抛物线上,
∴6=a(3+3)•(3-1),
∴a=
,
∴抛物线解析式为y=
x2+x-
.
(2)由y=
x2+x-
=
(x+1)2-2,
∴抛物线顶点P的坐标为(-1,-2),对称轴方程为x=-1.
设直线AC的解析式为y=kx+b,
∵A(3,6),C(-3,0)在该直线上,
∴
解得
,
∴直线AC的解析式为:y=x+3.
将x=-1代入y=x+3
得y=2,
∴G点坐标为(-1,2).
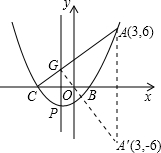
(3)作A关于x轴的对称点A′(3,-6),
连接A′G,A′G与x轴交于点M即为所求的点.
设直线A′G的解析式为y=kx+b.
∴
解得
,
∴直线A′G的解析式为y=-2x,令x=0,则y=0.
∴M点坐标为(0,0).
得x1=-3,x2=1.
∴抛物线与x轴的两个交点坐标为:C(-3,0),B(1,0),
设抛物线的解析式为y=a(x+3)(x-1).
∵A(3,6)在抛物线上,
∴6=a(3+3)•(3-1),
∴a=
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)由y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴抛物线顶点P的坐标为(-1,-2),对称轴方程为x=-1.
设直线AC的解析式为y=kx+b,
∵A(3,6),C(-3,0)在该直线上,
∴
|
|
∴直线AC的解析式为:y=x+3.
将x=-1代入y=x+3
得y=2,
∴G点坐标为(-1,2).

(3)作A关于x轴的对称点A′(3,-6),
连接A′G,A′G与x轴交于点M即为所求的点.
设直线A′G的解析式为y=kx+b.
∴
|
|
∴直线A′G的解析式为y=-2x,令x=0,则y=0.
∴M点坐标为(0,0).
点评:本题主要考查了用待定系数法求一次函数与二次函数解析式的方法.
(3)中先确定M点的位置是解题的关键.
(3)中先确定M点的位置是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
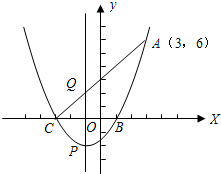 轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).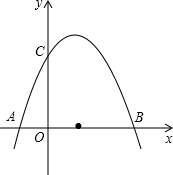 横坐标,此抛物线与y轴的正半轴交于点C.
横坐标,此抛物线与y轴的正半轴交于点C.