题目内容
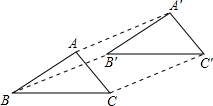
如图,把菱形ABCD沿着BD的方向平移到菱形A′B′C′D/′的位置.
(1)求证:重叠部分的四边形B′EDF是菱形;
(2)若重叠部分的四边形B′EDF′面积是把菱形ABCD面积的一半,且BD=
,求则此菱形移动的距离.
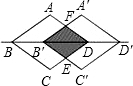
(1)求证:重叠部分的四边形B′EDF是菱形;
(2)若重叠部分的四边形B′EDF′面积是把菱形ABCD面积的一半,且BD=
| 2 |

(1)证明:有平移的特征知A′B′∥AB,又CD∥AB,
∴A′B′∥CD,同理B′C′∥AD.
∴四边形BEDF为平行四边形.
∵四边形ABCD是菱形,
∴AB=AD.
∴∠ABD=∠ADB.
又∵∠A′B′D=∠ABD,
∴∠A′B′D=∠ADB.
∴FB′=FD.
∴四边形B′EDF为菱形.
(2)∵菱形B′EDF与菱形ABCD有一个公共角,
∴此两个菱形对应角相等又对应边成比例.
∴此两个菱形相似.
∵S菱形ABCD:S菱形FB'ED=2:1,
∴
=
.
∴B′D=
×
=1.
∴平移的距离BB′=BD-B′D=
-1.
∴A′B′∥CD,同理B′C′∥AD.
∴四边形BEDF为平行四边形.
∵四边形ABCD是菱形,
∴AB=AD.
∴∠ABD=∠ADB.
又∵∠A′B′D=∠ABD,
∴∠A′B′D=∠ADB.
∴FB′=FD.
∴四边形B′EDF为菱形.
(2)∵菱形B′EDF与菱形ABCD有一个公共角,
∴此两个菱形对应角相等又对应边成比例.
∴此两个菱形相似.
∵S菱形ABCD:S菱形FB'ED=2:1,
∴
| B′D |
| BD |
|
∴B′D=
| ||
| 2 |
| 2 |
∴平移的距离BB′=BD-B′D=
| 2 |

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目