题目内容
动手操作: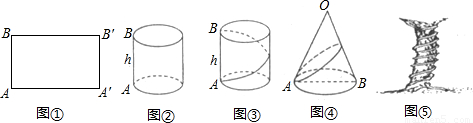
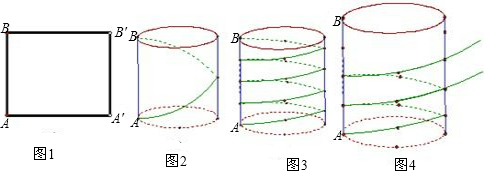
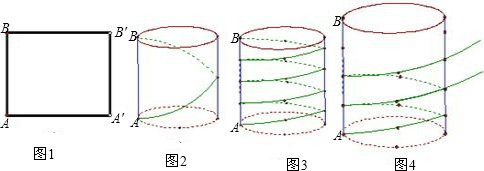
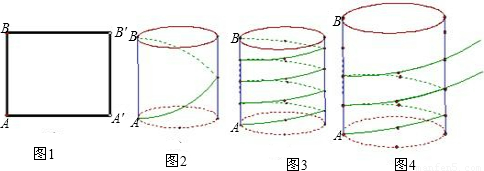
如图①,把长为l、宽为h的矩形卷成以AB为高的圆柱形,则点A′与点______重合,点B′与B′点______重合;
探究发现:
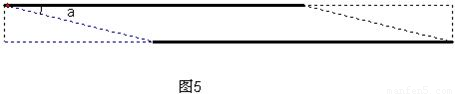
如图②,圆柱的底面周长是40,高是30,若在圆柱体的侧面绕一圈丝线作装饰,从下底面A出发,沿圆柱侧面绕一周到上底面B,则这条丝线最短的长度是______;
实践与应用:
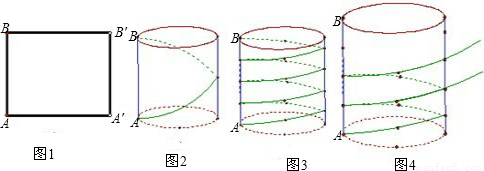
如图③,圆锥的母线长为4,底面半径为
 ,若在圆锥体的侧面绕一圈彩带做装饰,从圆锥的底面上的点A出发,沿圆锥侧面绕一周回到点A.求这条彩带最短的长度是多少?
,若在圆锥体的侧面绕一圈彩带做装饰,从圆锥的底面上的点A出发,沿圆锥侧面绕一周回到点A.求这条彩带最短的长度是多少?拓展联想:
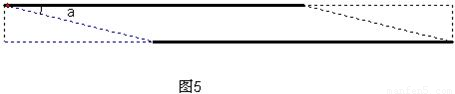
如图④,一颗古树上下粗细相差不大,可以看成圆柱体.测得树干的周长为3米,高为18米,有一根紫藤自树底部均匀的盘绕在树干上,恰好绕8周到达树干的顶部,你能求出这条紫藤至少有多少米吗?
【答案】分析:容易得出点A与点A′,B与B′重合;
矩形的对角线即为这条丝线最短的长度,由勾股定理即可得出答案;
连接AA′,根据弧长公式可得出圆心角的度数,由勾股定理可得出AA′;
将大树近似的看作圆柱将其展开,可得出紫藤的最短长度.
解答:解:动手操作:易得点A与点A′,B与B′重合;
探究与发现:圆柱的底面周长是矩形的长,
∵圆柱的底面周长是40,高是30,
∴矩形的对角线为50,
∴这条丝线最短的长度是 50,
实践与应用:
连接AA′,
∵底面周长为 π,∴弧长=
π,∴弧长= =
= π,
π,
∴n=120°即∠AOA′=120°,
∴∠A=30°,
作OB⊥AA′于B,在Rt△OBA中,
∵OA=4,∴OB=2,
∴AB=2 ,
,
∴AA′=4 ;
;
拓展联想:
方法一:如图,紫藤的长为: =30米;
=30米;
方法二:紫藤绕树干的周长为: =
=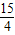 ,
,
则8周的周长为:8× =30米,
=30米,
故答案为A,B,50.
点评:本题考查了圆锥的计算、圆柱的计算以及其实际应用,综合性较强难度偏大.
矩形的对角线即为这条丝线最短的长度,由勾股定理即可得出答案;
连接AA′,根据弧长公式可得出圆心角的度数,由勾股定理可得出AA′;
将大树近似的看作圆柱将其展开,可得出紫藤的最短长度.
解答:解:动手操作:易得点A与点A′,B与B′重合;
探究与发现:圆柱的底面周长是矩形的长,
∵圆柱的底面周长是40,高是30,

∴矩形的对角线为50,
∴这条丝线最短的长度是 50,
实践与应用:
连接AA′,
∵底面周长为
 π,∴弧长=
π,∴弧长= =
= π,
π,∴n=120°即∠AOA′=120°,
∴∠A=30°,
作OB⊥AA′于B,在Rt△OBA中,
∵OA=4,∴OB=2,
∴AB=2
 ,
,∴AA′=4
 ;
;拓展联想:
方法一:如图,紫藤的长为:
 =30米;
=30米;
方法二:紫藤绕树干的周长为:
 =
=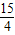 ,
,则8周的周长为:8×
 =30米,
=30米,故答案为A,B,50.
点评:本题考查了圆锥的计算、圆柱的计算以及其实际应用,综合性较强难度偏大.

练习册系列答案
相关题目