题目内容
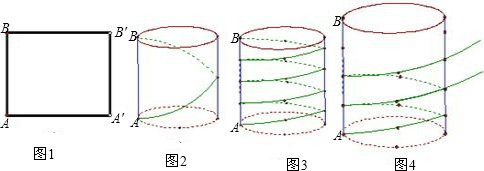
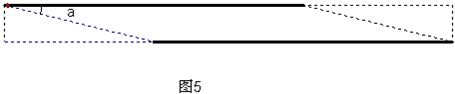
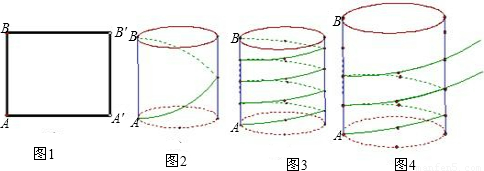
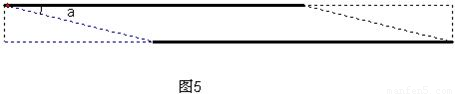
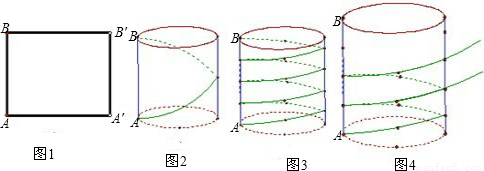
动手操作：如图1，把矩形AA′B′B卷成以AB为高的圆柱形，则点A与点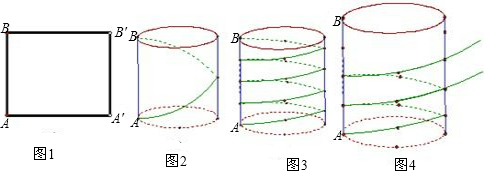
探究与发现：
（1）如图2，若圆柱的底面周长是30cm，高是40cm，从圆柱底部A处沿侧面缠绕一圈丝带到顶部B处作装饰，则这条丝线的最小长度是
（2）如图3，若用丝线从该圆柱的底部A缠绕4圈直到顶部B处，则至少需要多少丝线？
实践与应用：
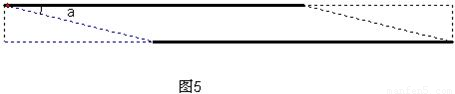
如图4，现有一个圆柱形的玻璃杯，准备在杯子的外面缠绕一层装饰带，为使带子全部包住杯子且不重叠，需要将带子的两端沿AE，CF方向进行裁剪，如图5所示，若带子的宽度为1.5厘米，杯子的半径为6厘米，则sinα=
分析：（1）连接AB′，已知AA′=30，A′B′=40，由勾股定理可求AB′的长；
（2）①在Rt△AA′C中，由勾股定理求AC，丝线至少为4×AC，②将剪开线MN与矩形短边的夹角α转化到直角三角形中，根据正弦的定义求值．
（2）①在Rt△AA′C中，由勾股定理求AC，丝线至少为4×AC，②将剪开线MN与矩形短边的夹角α转化到直角三角形中，根据正弦的定义求值．
解答：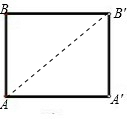
解：A′，B′；
探究与发现：
（1）如图，连接AB′，已知AA′=30，A′B′=40，由勾股定理，
得AB′=
=50；
（2）如图，在Rt△AA′C中，AA′=30，A′C=
=10，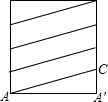
∴AC=
=
=10
，
∴丝线至少为4×AC=40
cm；
实践与应用：如图，沿MN把矩形剪开，矩形对角线AA′为杯子周长12π，带子的宽度A′M=1.5厘米，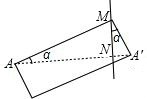
由互余关系可知∠A′MN=∠MAA′=α，
∴在Rt△AA′M中，sinα=
=
=
．
解：A′，B′；探究与发现：
（1）如图，连接AB′，已知AA′=30，A′B′=40，由勾股定理，
得AB′=
| AA′2+A′B′2 |
（2）如图，在Rt△AA′C中，AA′=30，A′C=
| 40 |
| 4 |
∴AC=
| AA′2+A′C2 |
| 302+102 |
| 10 |
∴丝线至少为4×AC=40
| 10 |
实践与应用：如图，沿MN把矩形剪开，矩形对角线AA′为杯子周长12π，带子的宽度A′M=1.5厘米，
由互余关系可知∠A′MN=∠MAA′=α，
∴在Rt△AA′M中，sinα=
| A′M |
| AA′ |
| 1.5 |
| 12π |
| 1 |
| 8π |
点评：本题考查了平面展开图形的运用．关键是明确立体图形与其平面展开图形之间的数量关系，充分运用勾股定理及三角函数的定义解题．
练习册系列答案
相关题目
