题目内容
已知抛物线y=-x2+2x+8与x轴交于B、C两点,点D平分BC.若在x轴上侧的A点为抛物线上的动点,且∠BAC为锐角,则AD的取值范围是分析:由“∠BAC为锐角”可知点A在以定线段BC为直径的圆外,又点A在x轴上侧,从而可确定动点A的范围,进而确定AD的取值范围.
解答: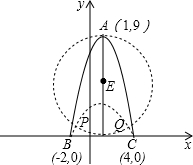 解:如图,∵抛物线y=-x2+2x+8,
解:如图,∵抛物线y=-x2+2x+8,
∴抛物线的顶点为A0(1,9),
对称轴为x=1,
与x轴交于两点B(-2,0)、C(4,0),
分别以BC、DA为直径作⊙D、⊙E,则
两圆与抛物线均交于两点P(1-2
,1)、Q(1+2
,1).
可知,点A在不含端点的抛物线
内时,∠BAC<90°,
且有3=DP=DQ<AD≤DA0=9,
即AD的取值范围是3<AD≤9.
 解:如图,∵抛物线y=-x2+2x+8,
解:如图,∵抛物线y=-x2+2x+8,∴抛物线的顶点为A0(1,9),
对称轴为x=1,
与x轴交于两点B(-2,0)、C(4,0),
分别以BC、DA为直径作⊙D、⊙E,则
两圆与抛物线均交于两点P(1-2
| 2 |
| 2 |
可知,点A在不含端点的抛物线
 |
| PA0Q |
且有3=DP=DQ<AD≤DA0=9,
即AD的取值范围是3<AD≤9.
点评:此题主要考查了抛物线与x轴的交点,解题时首先求出抛物线的顶点坐标和与x轴的交点坐标,然后利用已知条件探究即可解决问题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.