Question

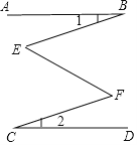
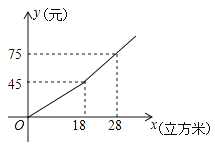
【题目】（1）如图1，若AB∥CD，将点P在AB、CD内部，∠B，∠D，∠P满足的数量关系是　 　，并说明理由．

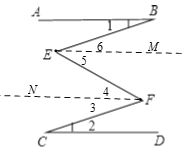
（2）在图1中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图2，利用（1）中的结论（可以直接套用），求∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？

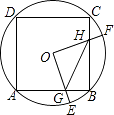
（3）科技活动课上，雨轩同学制作了一个图（3）的“飞旋镖”，经测量发现∠PAC＝30°，∠PBC＝35°，他很想知道∠APB与∠ACB的数量关系，你能告诉他吗？说明理由．

Answer 1

【答案】（1）∠BPD＝∠B+∠D；（2）∠BPD＝∠B+∠D+∠BQD；（3）∠APB＝65°+∠ACB．

【解析】

（1）过P作平行于AB的直线，根据内错角相等可得出三个角的关系．

（2）连接QP并延长至F，根据三角形的外角性质可得∠BPD﹑∠B﹑∠D﹑∠BQD的关系；

（3）连接CP并延长至G，根据三角形的外角性质可得∠APB﹑∠B﹑∠A﹑∠ACB的关系，代入即可．

（1）∠BPD＝∠B+∠D，如图1，过P点作PE∥AB，

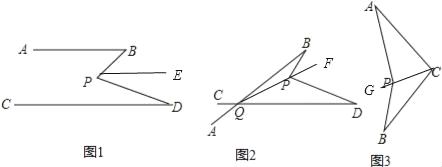
∵AB∥CD，∴CD∥PE∥AB，∴∠BPE＝∠B，∠EPD＝∠D．

∵∠BPD＝∠BPE+∠EPD，∴∠BPD＝∠B+∠D．

故答案为：∠BPD＝∠B+∠D；

（2）∠BPD＝∠B+∠D+∠BQD，连接QP并延长至F，如图2．

∵∠BPF＝∠ABP+∠BAP，∠FPD＝∠PDQ+∠PQD，∴∠BPD＝∠B+∠D+∠BQD；

（3）∠APB＝65°+∠ACB，连接CP并延长至G，如图3．

∵∠APG＝∠A+∠ACP，∠BPG＝∠B+∠BCP，∴∠APB＝∠B+∠A+∠ACB．

∵∠A＝30°，∠B＝35°，∴∠APB＝65°+∠ACB．