题目内容
为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹,下面是甲、乙两人各自的射击情况记录(其中乙的情况记录表上射中9、10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9、10环的子弹数均不为0发):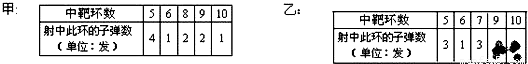
(1)求甲同学在这次测验中平均每次射中的环数;
(2)根据这次测验的情况,如果你是教练,你认为选谁参加比赛比较合适,并说明理由.(结果保留到小数点后第1位)
【答案】分析:(1)只要运用求平均数公式: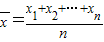 即可求出平均数,平均数大的成绩好;
即可求出平均数,平均数大的成绩好;
(2)若平均数相同计算对应的方差后进行比较.
解答:解:(1)甲同学在这次测验中平均每次射中的环数v甲=(4×5+6+2×8+2×9+10)÷10=7(环);
(2)乙同学中9,10环的情况有两种:
①当乙中9环2次,10环1次时,
v乙=(3×5+6+3×7+2×9+10)÷10=7(环),
此时s2甲=[4×(7-5)2+(7-6)2+2×(7-8)2+2×(7-9)2+(7-10)2]÷10=3.6
s2乙=[3×(7-5)2+(7-6)2+3×(7-7)2+2×(7-9)2+(7-10)2]÷10=3
∵s2甲>s2乙
∴选乙去参加比赛;
②当乙中9环1次,10环2次时,v乙=(3×5+6+3×7+9+2×10)÷10=7.1环,
此时v甲<v乙,故选乙去参加比赛.
点评:一般地设n个数据,x1、x2…,xn的平均数为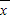 ,则方差S2=
,则方差S2=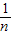 [(x1-
[(x1-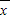 )2+(x2-
)2+(x2-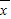 )2+…+(xn-
)2+…+(xn-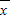 )2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
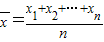 即可求出平均数,平均数大的成绩好;
即可求出平均数,平均数大的成绩好;(2)若平均数相同计算对应的方差后进行比较.
解答:解:(1)甲同学在这次测验中平均每次射中的环数v甲=(4×5+6+2×8+2×9+10)÷10=7(环);
(2)乙同学中9,10环的情况有两种:
①当乙中9环2次,10环1次时,
v乙=(3×5+6+3×7+2×9+10)÷10=7(环),
此时s2甲=[4×(7-5)2+(7-6)2+2×(7-8)2+2×(7-9)2+(7-10)2]÷10=3.6
s2乙=[3×(7-5)2+(7-6)2+3×(7-7)2+2×(7-9)2+(7-10)2]÷10=3
∵s2甲>s2乙
∴选乙去参加比赛;
②当乙中9环1次,10环2次时,v乙=(3×5+6+3×7+9+2×10)÷10=7.1环,
此时v甲<v乙,故选乙去参加比赛.
点评:一般地设n个数据,x1、x2…,xn的平均数为
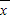 ,则方差S2=
,则方差S2=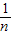 [(x1-
[(x1-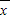 )2+(x2-
)2+(x2-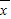 )2+…+(xn-
)2+…+(xn-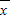 )2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立. 
练习册系列答案
相关题目
为了从甲、乙两名同学中选拔一人参加电脑知识竞赛,在相同条件下对他们的电脑知识进行了10次测验,成绩如下表:(单位:分)
回答下列问题:
(1)甲同学成绩的众数是 分,乙同学成绩的中位数是 分;
(2)若测验分数在85分以上为优秀,则甲同学的优秀率为 ,乙同学的优秀率为 ;
(3)若甲同学成绩的平均数为
甲,乙同学成绩的平均数为
乙,则有
甲
乙(填“>”、“<”或“=”);
(4)综合以上数据,你认为应该派哪一名同学参加电脑知识竞赛?并说明理由.
| 甲 | 76 | 84 | 90 | 86 | 81 | 87 | 86 | 82 | 85 | 93 |
| 乙 | 82 | 84 | 85 | 89 | 79 | 80 | 91 | 89 | 74 | 79 |
(1)甲同学成绩的众数是
(2)若测验分数在85分以上为优秀,则甲同学的优秀率为
(3)若甲同学成绩的平均数为
. |
| x |
. |
| x |
. |
| x |
. |
| x |
(4)综合以上数据,你认为应该派哪一名同学参加电脑知识竞赛?并说明理由.
