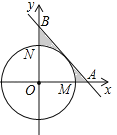题目内容
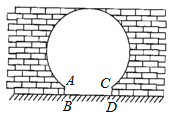
【题目】如图,已知直线MN与以AB为直径的半圆相切于点C,∠A=28°.
(1)求∠ACM的度数;
(2)在MN上是否存在一点D,使ABCD=ACBC,为什么?

【答案】(1)∠ACM=62°;(2)存在符合条件的点D,使ABCD=ACBC,理由见解析.
【解析】
(1)求∠ACM 的度数,需求出∠B 的度数;在![]() 中,已知∠A 的度数,即可求出∠B 、∠ACM 的度数;
中,已知∠A 的度数,即可求出∠B 、∠ACM 的度数;
(2)乘积的形式通常可以转化为比例的形式:
①![]() ,此时需证
,此时需证![]() ,那么过B作MN的垂线,那么垂足即为符合条件的D点;
,那么过B作MN的垂线,那么垂足即为符合条件的D点;
②![]() ,此时需证
,此时需证![]() ,则过A作MN的垂线,垂足也符合D点的条件.
,则过A作MN的垂线,垂足也符合D点的条件.
两者的证明过程一致,都是通过弦切角得出一组对应角相等,再加上一组直角得出三角形相似.
(1)∵AB是半圆的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠A=62°,
∵直线MN与以AB为直径的半圆相切于点C,
∴∠ACM=∠B=62°;
(2)存在符合条件的点D,使ABCD=ACBC,
①过A作AD⊥MN于D,则ABCD=ACBC,
证明:∵MN是半圆的切线,且切点为C,
∴∠ACD=∠B,
∵∠ADC=∠ACB=90°,
∴△ABC∽△ACD,
∴![]() ,
,
即ABCD=ACBC;
②过B作BD⊥MN于D,则ABCD=ACBC,
证明过程同①,
因此MN上存在至少一点D,使ABCD=ACBC.

练习册系列答案
相关题目