题目内容
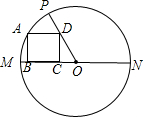
如图,点A,B,C,D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,求∠OAD+∠OCD的度数.


∵四边形ABCD是圆内接四边形,
∴∠B+∠D=180°.
∵四边形OABC为平行四边形,
∴∠AOC=∠B.
又∵由题意可知∠AOC=2∠ADC.
∴∠ADC=180°÷3=60°.
连接OD,可得AO=OD,CO=OD.
∴∠OAD=∠ODA,∠OCD=∠ODC.
∴∠OAD+∠OCD=∠ODA+∠ODC=∠D=60°.

∴∠B+∠D=180°.
∵四边形OABC为平行四边形,
∴∠AOC=∠B.
又∵由题意可知∠AOC=2∠ADC.
∴∠ADC=180°÷3=60°.
连接OD,可得AO=OD,CO=OD.
∴∠OAD=∠ODA,∠OCD=∠ODC.
∴∠OAD+∠OCD=∠ODA+∠ODC=∠D=60°.


练习册系列答案
相关题目