Question

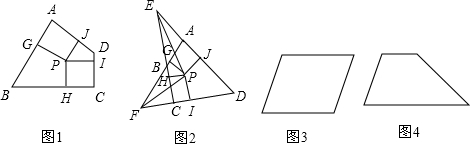
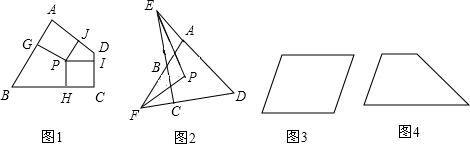
26、定义：到凸四边形一组对边距离相等，到另一组对边距离也相等的点叫凸四边形的准内点．如图1，PH=PJ，PI=PG，则点P就是四边形ABCD的准内点．

（1）如图2，∠AFD与∠DEC的角平分线FP，EP相交于点P．求证：点P是四边形ABCD的准内点．
（2）分别画出图3平行四边形和图4梯形的准内点．（作图工具不限，不写作法，但要有必要的说明）
（3）判断下列命题的真假，在括号内填“真”或“假”．
①任意凸四边形一定存在准内点．（

真

）
②任意凸四边形一定只有一个准内点．（

真

）
③若P是任意凸四边形ABCD的准内点，则PA+PB=PC+PD或PA+PC=PB+PD．（

假

）

Answer 1

分析：（1）过点P作PG⊥AB，PH⊥BC，PI⊥CD，PJ⊥AD，由角平分线的性质可知PJ=PH，PG=PI；
（2）平行四边形对角线的交点，即为平行四边形的准内点；梯形两腰夹角的平分线与梯形中位线的交点，即为梯形的准内点；
（3）①当凸四边形为平行四边形时，易知其对角线交点即为其准内点；②当凸四边形不为平行四边形时，可以将四边形的两边延长，构造三角形，其对角线交点即为准内点．

解答：解：（1）如图2，过点P作PG⊥AB，PH⊥BC，PI⊥CD，PJ⊥AD
∵EP平分∠DEC
∴PJ=PH．（3分）
同理PG=PI．（1分）
∴P是四边形ABCD的准内点．（1分）

（2）
（4分）
平行四边形对角线AC，BD的交点P₁就是准内点，如图3（1）．
或者取平行四边形两对边中点连线的交点P₁就是准内点，如图3（2）；
梯形两腰夹角的平分线与梯形中位线的交点P₂就是准内点．如图4．

（3）真；真；假．

点评：此题是一道新定义探索性题目，考查了对新信息的理解与应用能力，同时考查了三角形及四边形的性质．