题目内容
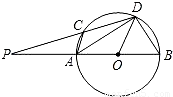
（2006•南充）如图，湖中有建筑物AB，某人站在建筑物顶部A在岸上的投影处C，发现自己的影长与身高相等．他沿BC方向走30m到D处，测得顶部A的仰角为30°，求建筑物AB的高．
【答案】分析：首先分析图形：根据题意构造直角三角形；本题涉及多个直角三角形，应利用其公共边构造三角关系，进而可求出答案．
解答：解：由C处人身高与影长相等可知，AB=CB．
设AB=xm，则BD=（x+30）m．
在Rt△ABD中，cotD=
，
∴ABcotD=BD．
xcot30°=x+30，
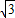x=x+30，
（
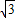-1）x=30，
∴x=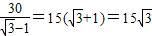
+15．
答：建筑物AB的高为（15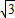
+15）m．
点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
解答：解：由C处人身高与影长相等可知，AB=CB．
设AB=xm，则BD=（x+30）m．
在Rt△ABD中，cotD=
，∴ABcotD=BD．
xcot30°=x+30，
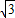x=x+30，（
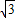-1）x=30，∴x=
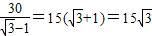+15．答：建筑物AB的高为（15
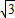+15）m．点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
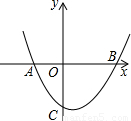
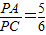，试求
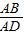的值．