题目内容
(2006•南充)如图,PAB,PCD是⊙O的两条割线,AB是⊙O的直径,AC∥OD.(1)求证:CD=______;(先填后证)
(2)若
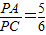 ,试求
,试求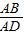 的值.
的值.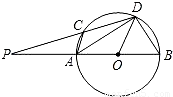
【答案】分析:(1)由于AC∥OD,OA=OD,故∠1=∠2,∠2=∠3.即∠1=∠3,则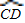 =
=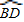 ,CD=BD;
,CD=BD;
(2)由于AC∥OD,故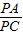 =
=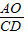 ,由于
,由于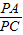 =
= ,CD=BD,故
,CD=BD,故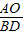 =
= ,因为AB=2AO,所以
,因为AB=2AO,所以 =
= ,又因为AB是⊙O的直径,所以∠ADB=90°,AD2+BD2=AB2,由
,又因为AB是⊙O的直径,所以∠ADB=90°,AD2+BD2=AB2,由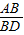 =
= ,设AB=5k,BD=3k,AD=4k,代入代数式即可求解.
,设AB=5k,BD=3k,AD=4k,代入代数式即可求解.
解答: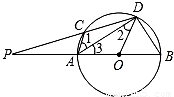 解:(1)求证:CD=BD,
解:(1)求证:CD=BD,
证明:∵AC∥OD,
∴∠1=∠2.
∵OA=OD,
∴∠2=∠3.
∴∠1=∠3.
∴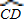 =
=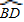 .
.
∴CD=BD.
(2)∵AC∥OD,
∴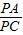 =
=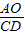 .
.
∵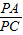 =
= ,CD=BD,
,CD=BD,
∴ =
= .
.
∵AB=2AO,
∴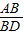 =
= .
.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴AD2+BD2=AB2
∵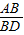 =
= ,设AB=5k,BD=3k,
,设AB=5k,BD=3k,
∴AD=4k.
∴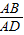 =
= .
.
点评:本题考查的是平行线的性质及圆周角定理,等腰三角形的,比较复杂,是一道具有综合性的题目.
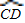 =
=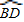 ,CD=BD;
,CD=BD;(2)由于AC∥OD,故
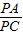 =
=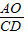 ,由于
,由于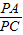 =
= ,CD=BD,故
,CD=BD,故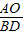 =
= ,因为AB=2AO,所以
,因为AB=2AO,所以 =
= ,又因为AB是⊙O的直径,所以∠ADB=90°,AD2+BD2=AB2,由
,又因为AB是⊙O的直径,所以∠ADB=90°,AD2+BD2=AB2,由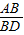 =
= ,设AB=5k,BD=3k,AD=4k,代入代数式即可求解.
,设AB=5k,BD=3k,AD=4k,代入代数式即可求解.解答:
 解:(1)求证:CD=BD,
解:(1)求证:CD=BD,证明:∵AC∥OD,
∴∠1=∠2.
∵OA=OD,
∴∠2=∠3.
∴∠1=∠3.
∴
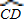 =
=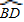 .
.∴CD=BD.
(2)∵AC∥OD,
∴
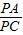 =
=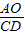 .
.∵
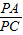 =
= ,CD=BD,
,CD=BD,∴
 =
= .
.∵AB=2AO,
∴
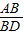 =
= .
.∵AB是⊙O的直径,
∴∠ADB=90°.
∴AD2+BD2=AB2
∵
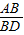 =
= ,设AB=5k,BD=3k,
,设AB=5k,BD=3k,∴AD=4k.
∴
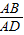 =
= .
.点评:本题考查的是平行线的性质及圆周角定理,等腰三角形的,比较复杂,是一道具有综合性的题目.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目