题目内容
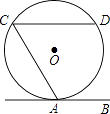
【题目】已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC. 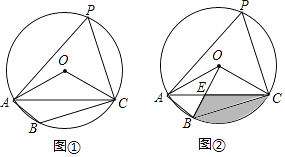
(1)如图①,求∠OCA的度数;
(2)如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ![]() ,求BC的长和阴影部分的面积.
,求BC的长和阴影部分的面积.
【答案】
(1)解:∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°
(2)解:∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC﹣∠AOB=90°,
在Rt△OCE中,OC=2 ![]() ,
,
∴OE=OCtan∠OCE=2 ![]() tan30°=2
tan30°=2 ![]() ×
× ![]() =2,
=2,
∴S△OEC= ![]() OEOC=
OEOC= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() ,
,
∴S扇形OBC= ![]() =3π,
=3π,
∴S阴影=S扇形OBC﹣S△OEC=3π﹣2 ![]()
【解析】(1)根据四边形ABCD是⊙O的内接四边形得到∠ABC+∠D=180°,根据∠ABC=2∠D得到∠D+2∠D=180°,从而求得∠D=60°,最后根据OA=OC得到∠OAC=∠OCA=30°;(2)由∠COB为直角,然后利用S阴影=S扇形OBC﹣S△OEC求解.
【考点精析】掌握圆内接四边形的性质和扇形面积计算公式是解答本题的根本,需要知道把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目