题目内容
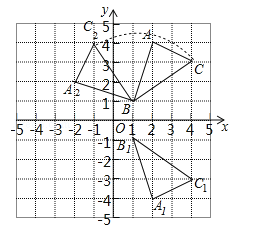
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).

(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1 、B1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中线段CC2所扫过的面积(结果保留根号和π).
【答案】(1)图形见解析(2)图形见解析(3)![]()
【解析】试题分析:(1)根据关于x轴对称的点的坐标特征,写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质,画出点A、C的对应点A2、C2,则可得到△A2BC2;
(3)C点旋转到C2点所经过的路径是以B点为圆心,BC为半径,圆心角为90°的弧,然后根据扇形面积公式计算即可.
试题解析:解:(1)如图,△A1B1C1为所作,点A1的坐标为(2,﹣4);
(2)如图,△A2BC2为所作;
(3)BC=![]() =
=![]() ,所以C C2扫过的面积=
,所以C C2扫过的面积=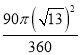 =
=![]() .
.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
