Question

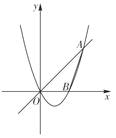
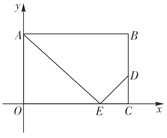
【题目】将矩形如图放置在平面直角坐标系中，为边上的一个动点，过点作交边于点，且，的长是方程的两个实数根，且．

（1）设，，求与的函数关系(不求的取值范围)；

（2）当为的中点时，求直线的解析式；

（3）在（2）的条件下，平面内是否存在点，使得以，，，为顶点的四边形为平行四边形？若存在，请直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）或；（3）存在．，，．

【解析】

（1）利用因式分解法解出一元二次方程，得到OA、OB的长，证明△AOE∽△ECD，根据相似三角形的性质列出比例式，整理得到y与x的函数关系；

（2）列方程求出OE，利用待定系数法求出直线AE的解析式；

（3）根据平行四边形的性质、坐标与图形性质解答．

（1），

，

∴解得，．

∵，

∴，．

∵，

∴∠AEO＋∠DEC＝90，

又∵∠AEO＋∠OAE＝90，

∴∠OAE＝∠CED，又∠AOE＝∠ECD＝90，

∴，

∴，

∴，

∴．

（2）当为的中点时，．

∵，

∴．

解得，．

当时，设直线的解析式为，把A（0，8），E（4，0）代入

得

解得，

∴；

当时，设直线的解析式为，把A（0，8），E（8，0）代入

得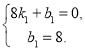

解得，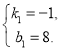

∴直线的解析式为或．

（3）当点F在线段OA上时，FA＝BD＝4，

∴OF＝4，即点F的坐标为（0，4），

当点F在线段OA的延长线上时，FA＝BD＝4，

∴OF＝12，即点F的坐标为（0，12），

当点F在线段BC右侧、AB∥DF时，DF＝AB＝12，

∴点F的坐标为（24，4），

综上所述，以A，D，B，F为顶点的四边形为平行四边形时，点F的坐标为（0，4）或（0，12）或（24，4）．