题目内容
【题目】如图,![]() 是半径为
是半径为![]() 的
的![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,
,![]() 为弧
为弧![]() 的中点,
的中点,![]() 是直径
是直径![]() 上一动点,则
上一动点,则![]() 的最小值为( )
的最小值为( )
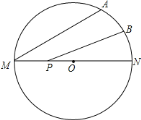
A. ![]() B.
B. ![]() C. 2 D. 4
C. 2 D. 4
【答案】B
【解析】
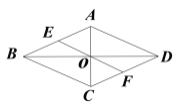
作点B关于MN的对称点B′,连接OA、OB′、AB′,根据轴对称确定最短路线问题,AB′与M的交点即为所求的使PA+PB的值最小的点,根据在同圆或等圆中,同弧所对的圆周角等于圆心角的一半求出∠AON=2∠AMN,再求出∠NOB′,然后求出∠AOB′=90°,从而判断出△AOB′是等腰直角三角形,根据等腰直角三角形的性质求解即可.
如图,作点B关于MN的对称点B′,连接OA、OB′、AB′,
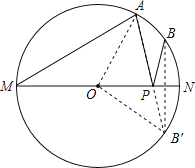
由轴对称确定最短路线问题可知,AB′与M的交点即为所求的使PA+PB的值最小的点,
∵![]()
∴![]() ∵B为弧AN的中点,
∵B为弧AN的中点,
∴![]()
∴![]()
∴△AOB′是等腰直角三角形,
∵⊙O的半径为2,
∴![]()
即PA+PB的最小值为为![]()
故选:B.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目