题目内容
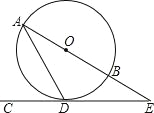
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线相交于点E,∠ADC=60°.
(1)求证:△ADE是等腰三角形;
(2)若AD=2![]() ,求BE的长.
,求BE的长.
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)连接OD,根据CD是⊙O的切线,推出∠ODC=90°,求出∠OAD=∠ODA=30°,根据三角形的外角性质求出∠E=∠A,即可得出答案;
(2)由(1)知,DE=DA=2![]() ,根据三角函数的定义求出OD,进一步求出OE,即可得到答案.
,根据三角函数的定义求出OD,进一步求出OE,即可得到答案.
试题解析:(1)连接OD,
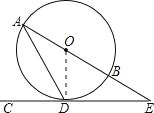
∵CD是⊙O的切线,
∴OD⊥CD,即∠ODC=90°,
∵∠ADC=60°,
∴∠ODA=30°,
在⊙O中OA=OD,
∴∠OAD=∠ODA=30°,
∴∠E=∠ADC-∠EAD=60°-30°=30°=∠EAD,
∴DA=DE,
即△ADE是等腰三角形.
(2)由(1)知,DE=DA=2![]() ,
,
在Rt△ODE中,OD=DE×tan30°=![]() =2,
=2,
OE=2OD=4,
∴BE=OE-OB=OE-OD=4-2=2,
答:BE的长是2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙、丙、丁四位同学五次100米跑成绩统计如下表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加县运动会,那么应选( )
甲 | 乙 | 丙 | 丁 | |
平均数(秒) | 16 | 15 | 15 | 16 |
方差 | 30 | 30 | 35 | 42 |
A. 甲B. 乙C. 丙D. 丁