题目内容
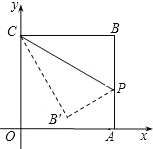
【题目】在平面直角坐标系中,四边形OABC是正方形,点A的坐标为(4,0).点P为边AB上一点,∠CPB=60°,沿CP折叠正方形后,点B落在平面内点B′处,则B′点坐标为( )
A.(4﹣2![]() ,2) B.(2,4﹣2
,2) B.(2,4﹣2![]() ) C.(2,1) D.(2,2﹣
) C.(2,1) D.(2,2﹣![]() )
)
【答案】B
【解析】
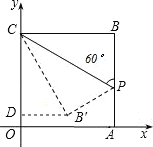
试题分析:过点B′作B′D⊥OC,因为∠CPB=60°,CB′=OC=OA=4,所以∠B′CD=30°,B′D=2,根据勾股定理得DC=2![]() ,故OD=4﹣2
,故OD=4﹣2![]() ,即B′点的坐标即可求解.
,即B′点的坐标即可求解.
解:过点B′作B′D⊥OC
∵∠CPB=60°,CB′=OC=OA=4
∴∠B′CD=30°,B′D=2
根据勾股定理得DC=2![]()
∴OD=4﹣2![]() ,即B′点的坐标为(2,4﹣2
,即B′点的坐标为(2,4﹣2![]() )
)
故选B.

练习册系列答案
相关题目