题目内容
如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连结EF、EB.

求证:△ABE≌△ACD;(4分)
求证:四边形EFCD是平行四边形.(5分)
【答案】
证明略
【解析】(1)证明:∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°——————2分
∴∠EAD-∠BAD=∠BAC-∠BAD
即:∠EAB=∠DAC ——————1分
∴△ABE≌△ACD(SAS) ——————1分
(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,又∵BF=DC,∴BE=BF.
∵△ABC是等边三角形,∴∠DCA=60°,
∴△BEF为等边三角形.
∴∠EFB=60°,EF=BF ————————2分
∵△ABC是等边三角形,∴∠ABC=60°, ∴∠ABC=∠EFB,
∴EF∥BC,即EF∥DC ————————1分
∵EF=BF,BF=DC,∴EF=DC ————————1分
∴四边形EFCD是平行四边形. ————————1分

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
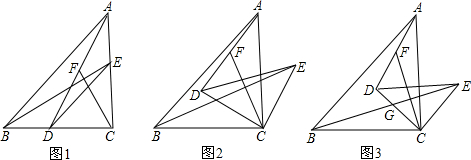
 10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点
10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点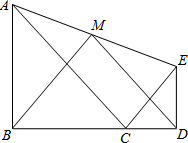 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.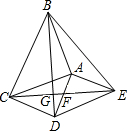 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中: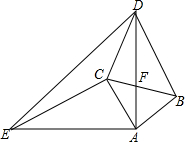 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.