题目内容
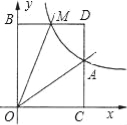
【题目】如图,已知反比例函数y=![]() 的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
(1)求反比例函数的解析式;
(2)当∠OAM=90°时,求点M的坐标.
【答案】(1)、y=![]() ;(2)、(
;(2)、(![]() ,4).
,4).
【解析】
试题分析:(1)、把A点坐标代入y=![]() 中求出k的值即可;(2)、先证明Rt△AMD∽Rt△OAC得到(n﹣1):2=(2﹣m):1,再利用点M(m,n)在y=
中求出k的值即可;(2)、先证明Rt△AMD∽Rt△OAC得到(n﹣1):2=(2﹣m):1,再利用点M(m,n)在y=![]() 的图象上得到n=
的图象上得到n=![]() ,然后解关于m的方程求出m,从而可得到M点的坐标.
,然后解关于m的方程求出m,从而可得到M点的坐标.
试题解析:(1)、把A(2,1)代入y=![]() 得k=2×1=2, 所以反比例函数解析式为y=
得k=2×1=2, 所以反比例函数解析式为y=![]() ;
;
(2)、∵∠OAM=90°, ∴∠MAD+∠CAO=90°, 而∠CAO+∠AOC=90°, ∴∠AOC=∠MAD,
∴Rt△AMD∽Rt△OAC, ∴AD:OC=MD:AC,即(n﹣1):2=(2﹣m):1,
∴n﹣1=4﹣2m, ∵点M(m,n)在y=![]() 的图象上, ∴n=
的图象上, ∴n=![]() , ∴
, ∴![]() ﹣1=4﹣2m,
﹣1=4﹣2m,
整理得2m2﹣5m+2=0,解得m1=![]() ,m2=2(舍去), ∴n=4, ∴点M的坐标为(
,m2=2(舍去), ∴n=4, ∴点M的坐标为(![]() ,4).
,4).

练习册系列答案
相关题目