题目内容
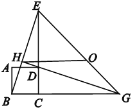
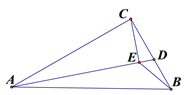
【题目】如图，菱形ABCD边长为4，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C的最小值是（ ）
A.2
B.+1C.2
﹣2D.3
【答案】C
【解析】
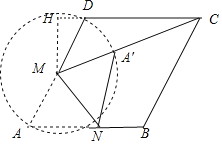
根据题意，在折叠过程中A′在以M为圆心、AD为直径的圆上的弧AD上运动，当A′C取最小值时，由两点之间线段最短知此时M、A′、C三点共线，得出A′的位置，过点M作MH⊥DC于点F，再利用含30°的直角三角形的性质以及勾股定理求出MC的长，进而求出A′C的长即可．
解：如图所示，∵MA′是定值，A′C长度取最小值时，即A′在MC上．
过点M作MH⊥DC于点F，
∵在边长为4的菱形ABCD中，∠A=60°，M为AD的中点，
∴2MD=AD=CD=4，∠HDM=∠A=60°，
∴MD=2，∠HMD=30°，
∴HD=
MD=1，∴HM=
=
，CH=CD+DH=5，
∴
，
∴A′C=MC-MA′=2
-2；
故选：C．
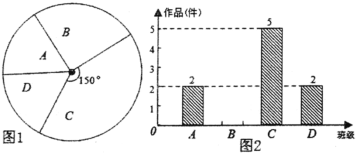
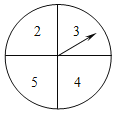
手拉手全优练考卷系列答案【题目】如图所示，有一个可以自由转动的转盘，其盘面分为4等份，在每一等份分别标有对应的数字2，3，4，5．小明打算自由转动转盘10次，现已经转动了8次，每一次停止后，小明将指针所指数字记录如下：
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
（1）求前8次的指针所指数字的平均数．
（2）小明继续自由转动转盘2次，判断是否可能发生“这10次的指针所指数字的平均数不小于3.3，且不大于3.5”的结果？若有可能，计算发生此结果的概率，并写出计算过程；若不可能，说明理由．（指针指向盘面等分线时为无效转次．）
【题目】我市某工艺厂为配合北京奥运，设计了一款成本为20元∕件的工艺品投放市场进行试销．经过调查，得到如下数据：
销售单价x（元/件） | … | 30 | 40 | 50 | 60 | … |
每天销售量y（件） | … | 500 | 400 | 300 | 200 | … |
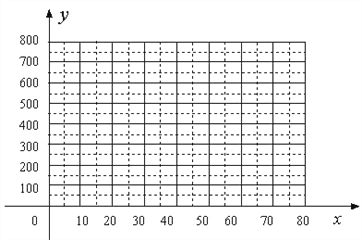
（1）把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；
（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？（利润=销售总价﹣成本总价）
（3）当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？
