题目内容
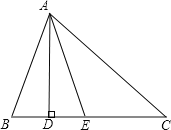
【题目】如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC.已知∠B=65°,∠DAE=20°,求∠C的度数.
【答案】25°
【解析】
试题分析:由垂直的定义得到∠ADB=90°,根据三角形的内角和得到∠BAD=90°﹣65°=25°,求得∠BAE=∠BAD+∠DAE=25°+20°=45°,根据角平分线的定义得到∠BAC=2∠BAE=2×45°=90°,根据三角形的内角和即可得到结论.
解:∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣65°=25°,
∴∠BAE=∠BAD+∠DAE=25°+20°=45°,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2×45°=90°,
∴∠C=180°﹣∠B﹣∠BAC=25°.

练习册系列答案
相关题目