题目内容
计算或解分式方程:
(1)直接写出结果:
•
=
,
+
=
(2)
-a-2
(3)
•
÷
(4)
÷(a-
)
(5)解方程:
+2=
(6)解方程:
-
=1.
(1)直接写出结果:
| 5ab |
| 3c |
| 12c2 |
| 5ab2 |
| 4c |
| b |
| 4c |
| b |
| x2 |
| x-y |
| y2 |
| y-x |
x+y
x+y
(2)
| 4 |
| a-2 |
(3)
| x2+6x+9 |
| x2-9 |
| x-3 |
| x+2 |
| x+3 |
| x |
(4)
| a-b |
| a |
| 2ab-b2 |
| a |
(5)解方程:
| x-4 |
| x-3 |
| 1 |
| 3-x |
(6)解方程:
| 3y-1 |
| y |
| 2y |
| y-1 |
分析:(1)利用分式的乘法法则运算即可求得结果,利用分式的加减运算法则求解即可求得答案,注意运算结果需化为最简;
(2)首先将原式化为
-(a+2),然后通分,再利用同分母得分是相加减的运算法则求解即可求得答案,注意运算结果需化为最简;
(3)首先将各多项式因式分解,然后利用分式的乘除运算法则求解即可求得答案;
(4)根据分式混合运算法则:先算括号里面的,再进行除法运算即可求得答案,注意运算结果需化为最简;
(5)观察可得最简公分母是(x-3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(6)观察可得最简公分母是y(y-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(2)首先将原式化为
| 4 |
| a-2 |
(3)首先将各多项式因式分解,然后利用分式的乘除运算法则求解即可求得答案;
(4)根据分式混合运算法则:先算括号里面的,再进行除法运算即可求得答案,注意运算结果需化为最简;
(5)观察可得最简公分母是(x-3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(6)观察可得最简公分母是y(y-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答:解:(1)
•
=
,
+
=
-
=
=
=x+y;
(2)
-a-2=
-(a+2)=
-
=
=-
;
(3)
•
÷
=
•
•
=
;
(4)
÷(a-
)=
÷
=
•
=
;
(5)方程两边同乘以(x-3)得:x-4+2(x-3)=-1,
解得:x=3,
检验:当x=3时,x-3=0,则x=3不是原分式方程的解,
故原分式方程无解;
(6)方程两边同乘以y(y-1)得:(3y-1)(y-1)-2y2=y(y-1),
解得:y=
,
检验:当y=
时,y(y-1)=-
≠0,则y=
是原分式方程的解,
故原分式方程的解为:y=
.
故答案为:(1)
;(2)x+y.
| 5ab |
| 3c |
| 12c2 |
| 5ab2 |
| 4c |
| b |
| x2 |
| x-y |
| y2 |
| y-x |
| x2 |
| x-y |
| y2 |
| x-y |
| x2-y2 |
| x-y |
| (x+y)(x-y) |
| x-y |
(2)
| 4 |
| a-2 |
| 4 |
| a-2 |
| 4 |
| a-2 |
| (a+2)(a-2) |
| a-2 |
| 4-a2+4 |
| a-2 |
| a2 |
| a-2 |
(3)
| x2+6x+9 |
| x2-9 |
| x-3 |
| x+2 |
| x+3 |
| x |
| (x+3)2 |
| (x+3)(x-3) |
| x-3 |
| x+2 |
| x |
| x+3 |
| x |
| x+2 |
(4)
| a-b |
| a |
| 2ab-b2 |
| a |
| a-b |
| a |
| a2-2ab+b2 |
| a |
| a-b |
| a |
| a |
| (a-b)2 |
| 1 |
| a-b |
(5)方程两边同乘以(x-3)得:x-4+2(x-3)=-1,
解得:x=3,
检验:当x=3时,x-3=0,则x=3不是原分式方程的解,
故原分式方程无解;
(6)方程两边同乘以y(y-1)得:(3y-1)(y-1)-2y2=y(y-1),
解得:y=
| 1 |
| 3 |
检验:当y=
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
故原分式方程的解为:y=
| 1 |
| 3 |
故答案为:(1)
| 4c |
| b |
点评:此题考查了分式的混合运算与分式方程的求解方法.注意解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解;解分式方程一定注意要验根;注意分式混合运算的运算顺序,注意运算结果要化为最简.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
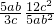 =______,
=______,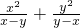 =______
=______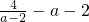
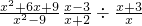
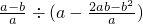
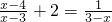
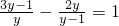 .
.