题目内容
如图直角梯形ABCD的中位线EF的长为a，垂直于底的腰AB长为b，则图中阴影部分的面积为
- A.a+b
- B.2ab
- C.ab
- D.
ab
D
分析：S△DEC=S△DEF+S△CEF=EF•AE+EF•BE=EF•AB即可求解．
解答：S△DEC=S△DEF+S△CEF=EF•AE+EF•BE=EF•AB=ab．
故选D．
点评：本题考查了三角形的面积公式，正确理解S△DEC=S△DEF+S△CEF=EF•AE+EF•BE=EF•AB是关键．
分析：S△DEC=S△DEF+S△CEF=
EF•AE+EF•BE=EF•AB即可求解．解答：S△DEC=S△DEF+S△CEF=
EF•AE+EF•BE=EF•AB=ab．故选D．
点评：本题考查了三角形的面积公式，正确理解S△DEC=S△DEF+S△CEF=
EF•AE+EF•BE=EF•AB是关键． 
练习册系列答案
相关题目
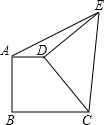如图直角梯形ABCD中，AD∥BC，AB⊥BC，∠BCD=45°，AD=2，BC=3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，则△ADE的面积是（ ）
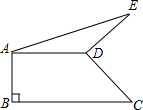如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=1，BC=3，以D为旋转中心，CD逆时针旋转90°得DE，则AE=
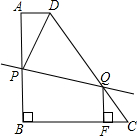如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=8，CD=10．
如图直角梯形ABCD的中位线EF的长为a，垂直于底的腰AB长为b，则图中阴影部分的面积为（ ）