题目内容
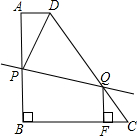 如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.
如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.(1)求BC的长;
(2)动点P从点B出发,以1cm/s的速度沿B→A→D方向向点D运动;动点Q从点C出发,以1cm/s的速度沿C→D方向向点D运动;过点Q作QF⊥BC于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之结束,设运动时间为t秒.问:在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
分析:(1)过点D作DE⊥BC于点E,然后求出AD=BE=2,AB=DE=8,在Rt△DEC中,根据CE=
求出CE,即可求出BC的长;
(2)(i)当0≤t≤8时,过点Q作QG⊥AB于点G,过点Q作QF⊥CB于点F,根据△CQF∽△CDE得出
=
=
,所以CF=
t,QF=
t,所以PG=t-
t=
t,QG=8-
t,然后分别用t表示出PD2=t2-16t+68,PQ2=
t 2-
t+64,若DQ=PD,则(10-t)2=t2-16t+68,若DQ=PQ,则(10-t)2=
t 2-
t+64,最后解方程即可;
(ii)当8<t<10时,PD=DQ=10-t,此时以DQ为一腰的等腰△DPQ恒成立;而当t=10时,点P、D、Q三点重合,无法构成三角形;
(iii)当10<t≤12时,PD=DQ=t-10,此时以DQ为一腰的等腰△DPQ恒成立,从而得出最后答案.
| CD2-DE 2 |
(2)(i)当0≤t≤8时,过点Q作QG⊥AB于点G,过点Q作QF⊥CB于点F,根据△CQF∽△CDE得出
| QF |
| DE |
| CG |
| CD |
| CF |
| CE |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 48 |
| 5 |
| 2 |
| 5 |
| 48 |
| 5 |
(ii)当8<t<10时,PD=DQ=10-t,此时以DQ为一腰的等腰△DPQ恒成立;而当t=10时,点P、D、Q三点重合,无法构成三角形;
(iii)当10<t≤12时,PD=DQ=t-10,此时以DQ为一腰的等腰△DPQ恒成立,从而得出最后答案.
解答: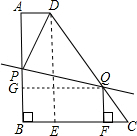 解:(1)过点D作DE⊥BC于点E
解:(1)过点D作DE⊥BC于点E
∵四边形ABCD是直角梯形
∴四边形ABED是矩形
∴AD=BE=2,AB=DE=8
在Rt△DEC中,CE=
=
=6
∴BC=8.
(2)(i)当0≤t≤8时,过点Q作QG⊥AB于点G,过点Q作QF⊥CB于点F.
∵BP=t,CQ=t,
∴AP=8-t,DQ=10-t,
∵DE⊥BC,QF⊥CB
∴△CQF∽△CDE
∴
=
=
,
∴
=
=
,
∴CF=
t,QF=
t,
∴PG=t-
t=
t,QG=8-
t,
∴PD2=AP2+AD2=(8-t)2+22=t2-16t+68,
∴PQ2=QG2+PG2=(8-
t)2+(
t)2=
t 2-
t+64,
若DQ=PD,则DQ2=PD2,
(10-t)2=t2-16t+68,
解得:t=8;
若DQ=PQ,则DQ2=PQ2,
(10-t)2=
t 2-
t+64,
解得:t1=
,t2=
>8(舍去),
此时t=
.
(ii)当8<t<10时,PD=DQ=10-t,
∴此时以DQ为一腰的等腰△DPQ恒成立;
而当t=10时,点P、D、Q三点重合,无法构成三角形;
(iii)当10<t≤12时,PD=DQ=t-10,
此时以DQ为一腰的等腰△DPQ恒成立;
综上,当t=
或8≤t<10或10<t≤12时,以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形.
 解:(1)过点D作DE⊥BC于点E
解:(1)过点D作DE⊥BC于点E∵四边形ABCD是直角梯形
∴四边形ABED是矩形
∴AD=BE=2,AB=DE=8
在Rt△DEC中,CE=
| CD2-DE 2 |
| 10 2-8 2 |
∴BC=8.
(2)(i)当0≤t≤8时,过点Q作QG⊥AB于点G,过点Q作QF⊥CB于点F.
∵BP=t,CQ=t,
∴AP=8-t,DQ=10-t,
∵DE⊥BC,QF⊥CB
∴△CQF∽△CDE
∴
| QF |
| DE |
| CQ |
| CD |
| CF |
| CE |
∴
| QF |
| 8 |
| t |
| 10 |
| CF |
| 6 |
∴CF=
| 3 |
| 5 |
| 4 |
| 5 |
∴PG=t-
| 4 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
∴PD2=AP2+AD2=(8-t)2+22=t2-16t+68,
∴PQ2=QG2+PG2=(8-
| 3 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 48 |
| 5 |
若DQ=PD,则DQ2=PD2,
(10-t)2=t2-16t+68,
解得:t=8;
若DQ=PQ,则DQ2=PQ2,
(10-t)2=
| 2 |
| 5 |
| 48 |
| 5 |
解得:t1=
26-2
| ||
| 3 |
26+2
| ||
| 3 |
此时t=
26-2
| ||
| 3 |
(ii)当8<t<10时,PD=DQ=10-t,
∴此时以DQ为一腰的等腰△DPQ恒成立;
而当t=10时,点P、D、Q三点重合,无法构成三角形;
(iii)当10<t≤12时,PD=DQ=t-10,
此时以DQ为一腰的等腰△DPQ恒成立;
综上,当t=
26-2
| ||
| 3 |
点评:本题主要考查了相似三角形的性质和判定,关键是列出方程,并对求出的结果与本题相结合,要注意的是(2)中,要根据P点的不同位置进行分类求解.

练习册系列答案
相关题目
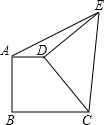 如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )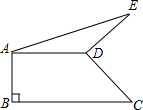 如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=1,BC=3,以D为旋转中心,CD逆时针旋转90°得DE,则AE=
如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=1,BC=3,以D为旋转中心,CD逆时针旋转90°得DE,则AE= 如图直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB长为b,则图中阴影部分的面积为( )
如图直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB长为b,则图中阴影部分的面积为( )