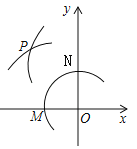题目内容
【题目】已知抛物线y=x2-2mx+4m-8的顶点为A
(1) 求证:该抛物线与x轴总有两个交点
(2) 当m=1时,直线BC:y=kx-2与该抛物线交于B、C两点,若线段BC被x轴平分,求k的值
(3) 以A为一个顶点作该抛物线的内接正三角形AMN(M、N两点在抛物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由

【答案】(1)证明见解析(2)k=-1±![]() (3) S△AMN=3
(3) S△AMN=3![]() 为定值
为定值
【解析】试题分析:(1)根据根的判别式可证明交点的个数;
(2)把m=1代入函数的解析式,然后根据二次函数和一次函数的交点,联立方程组,得到含k的关于x的一元二次方程,然后根据根与系数的关系求出k的值;
(3)根据函数和等边三角形的对称性得到AB的关系式,然后根据三角形的面积确定其为定值.
试题解析:(1) ∵△=4m2-4(4m-1)=4(m-2)2+16>0
∴该抛物线与x轴总有两个交点
(2) 当m=1时,y=x2-2x-4
设A(x1,y1)、B(x2,y2)
联立![]() ,整理得x2-(k+2)x-2=0
,整理得x2-(k+2)x-2=0
∴x1+x2=k+2,x1x2=-2
当线段BC被x轴平分时
∴y1+y2=k(x1+x2)-4=0
∴k(k+2)-4=0,解得k=-1±![]()
(3) 根据抛物线和正三角形的对称性,可知MN⊥y轴,设抛物线的对称轴与MN交于点B
则AB=![]() BM
BM
设M(a,b)
∴BM=a-m(m<a)
又AB=yB-yA=b-(4m-8-m2)=a2-2ma+4m-8-(4m-8-m2)=(a-m)2
∴(a-m)2=![]() (a-m),∴a-m=
(a-m),∴a-m=![]()
∴BM=![]() ,AB=3
,AB=3
∴S△AMN=![]() AB·2BM=
AB·2BM=![]() ×3×2×
×3×2×![]() =3
=3![]() 为定值
为定值


练习册系列答案
相关题目