题目内容
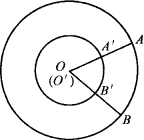
如图,在两半径不同的同心圆中,∠AOB=∠A′OB′=60°,则( )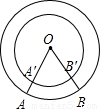
A.
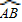 =
=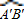
B.
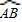 >
>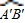
C.
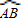 的度数=
的度数=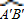 的度数
的度数D.
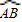 的长度=
的长度=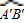 的长度
的长度
【答案】分析:根据圆心角的度数等于它所对的弧的度数,由∠AOB=∠A′OB′=60°,得到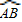 的度数=
的度数= 的度数=60°,根据弧长公式得到
的度数=60°,根据弧长公式得到
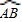 的长度=
的长度=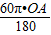 ,而
,而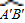 的长度=
的长度=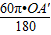 ,从而可对选项进行判断.
,从而可对选项进行判断.
解答:解:∵∠AOB=∠A′OB′=60°,
∴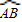 的度数=
的度数=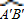 的度数=60°,
的度数=60°,
∵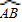 的长度=
的长度=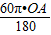 ,而
,而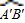 的长度=
的长度=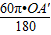 ,
,
而OA′<OA,
所以A,B,D选项不正确,C选项正确.
故选C.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等,也考查了等弧的概念.
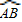 的度数=
的度数= 的度数=60°,根据弧长公式得到
的度数=60°,根据弧长公式得到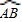 的长度=
的长度=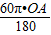 ,而
,而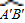 的长度=
的长度=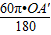 ,从而可对选项进行判断.
,从而可对选项进行判断.解答:解:∵∠AOB=∠A′OB′=60°,
∴
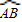 的度数=
的度数=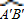 的度数=60°,
的度数=60°,∵
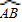 的长度=
的长度=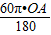 ,而
,而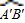 的长度=
的长度=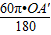 ,
,而OA′<OA,
所以A,B,D选项不正确,C选项正确.
故选C.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等,也考查了等弧的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
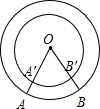 如图,在两半径不同的同心圆中,∠AOB=∠A′OB′=60°,则( )
如图,在两半径不同的同心圆中,∠AOB=∠A′OB′=60°,则( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|

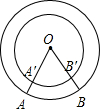 如图,在两半径不同的同心圆中,∠AOB=∠A′OB′=60°,则
如图,在两半径不同的同心圆中,∠AOB=∠A′OB′=60°,则 =
=
 (A)
(A)